Locos por la Geología

Archivo de la categoría ‘Geología para principiantes’

Para poder seguir avanzando en el reconocimiento de las medidas de nuestro planeta, es importante que repasen dos posts anteriores, o más propiamente dicho, un post en dos entregas.

En la primera parte, les expliqué la Ley de la Gravitación Universal, que será la base teórica de lo que analizaremos hoy, y sin la cual no entenderán nada. En la segunda, les adelanté una descripción muy general del experimento con que se «pesó» la Tierra, y que prometí aclarar en detalle más adelante, que es precisamente lo que me dispongo a hacer ahora.

¿Con qué datos se contaba antes de esta medición?

Como habrán visto en los posts que les mandé a leer, se tenía clara la fórmula de la gravedad universal, donde figuraba la Constante de la Gravedad, pero ésta era desconocida hasta la experiencia que hoy nos ocupa.

Por otra parte, ya desde muchos siglos antes se conocía la longitud del arco de meridiano, gracias a la determinación de Eratóstenes que les conté en este otro post .

Conocer la longitud del arco de meridiano permitió a su vez definir la circunferencia de la Tierra, según las inferencias que les mostré en la parte 1 del post que he linkeado más arriba.

Ahora bien, una vez que se conoce el perímetro de la circunferencia, sólo es cuestión de aplicar un par de fórmulas básicas y sencillas de la Geometría para obtener datos que necesitamos para «pesar» la Tierra.

Sabemos que el perímetro de la circunferencia (Pc) es:

Pc= π . d

donde π es pi, de valor conocido; y d es el diámetro (o dos veces el radio) de la Tierra, que buscamos conocer. Despejando pues en la fórmula, resulta:

d= Pc/ π

Y una vez que se ha calculado el radio r (que es la mitad del diámetro), sólo hay que usarlo en la fórmula del volumen de la esfera (Ve).

Ve= 4/3 π . r³

El volumen resultante al aplicar la fórmula con los valores del planeta, fue de 1,0842 x 10⁸ km³. Por supuesto que se trata de un volumen sólo aproximado, porque, como también les he explicado, la Tierra dista mucho de ser una simple pelota. Más bien se da el lujo de tener una forma propia a la que llamamos geoide, pero cuyo volumen podemos a través de esa fórmula medianamente estimar. Y todavía hacemos otra concesión, ya que en lo que sigue, pensaremos el volumen como equivalente a la masa, porque en cierta medida lo es.

Aδun con todas estas dispensas, ya contamos con una parte de los datos que requerimos para conocer la densidad (δ) de la Tierra. Como sabemos que densidad es el cociente entre la masa y el volumen, bastará con determinar la masa para conocer su densidad según la fórmula:

δ= M/V

donde δ es densidad; M es masa y V es volumen.

¿En qué consiste el experimento de Cavendish?

Ya les dije en uno de los posts que les mandé a leer, que el experimento con el que se pretendió «pesar la Tierra» fue ideado por Lord Cavendish en 1798, en su casa de Clapham Common. En los hechos, no fue la masa de la Tierra lo que determinó en realidad con ese experimento, sino el valor de la constante Universal de la Gravedad (G), pero una vez que se conoció ésta, el paso siguiente fue muy sencillo, y ya pudo conocerse el valor de la masa terrestre agregando sólo un datito más.

El punto de partida es la fórmula de F que es la fuerza de atracción gravitacional.

F= G. m.m’ / r²

Recordemos que F es la fuerza de atracción que se ejerce siempre entre dos cuerpos cualquiera.

m es la masa de uno de los cuerpos sometidos a esa fuerza.

m’ es la masa del otro cuerpo.

r es la distancia que separa ambos cuerpos.

Ahora veamos la construcción de la balanza de Cavendish, que es la que se ve en la ilustración superior. Este aparato consta de dos masas m y m’ , cada una de las cuales está a su vez dividida en dos esferas de plomo, pequeñas en el caso de m, y grandes en el caso de m’, pero todas de valor conocido.

Las dos bolas que forman la masa m están suspendidas de una estructura que al impedirles caer, las independiza de la atracción gravitacional terrestre, y las hace en cambio dependientes en su movimiento, sólo de la atracción gravitacional ejercida por las otras dos esferas que suman la masa m’. Éstas, a su vez, están sustentadas sobre un plato que les permite girar pero no caerse.

En definitiva, las esferitas solamente pueden girar alrededor de los ejes de los aparejos que las sostienen, y lo hacen en respuesta a la fuerza gravitatoria F que se genera entre ambas masas m y m’. Obviamente, esa fuerza responde a la fórmula general de la gravedad ya repasda más arriba.

Como los detalles de construcción del aparato son todos conocidos, se sabe de antemano cuál es el valor de las masas m y m’, y también el del radio r que las separa. Para conocer G, hay que medir F y resolver la ecuación, que ahora pasará a ser:

G= F. r² / m.m’

Cavendish resolvió el problema de manera sencilla: el cable del cual penden las esferas que constituyen la masa m tiene un módulo de torsión conocido, es decir que gira un cierto ángulo bien determinado por cada unidad de fuerza aplicada. Estableciendo cuánto ha rotado el hilo se mide pues F. Ésa es la función del espejo solidario con el cable, y que a medida que más se tuerce éste, va reflejando la luz incidente sobre él, en una porción más alejada de la inicial, que se toma como cero, en la escala graduada.

Con todos los valores ya conocidos, se pudo establecer la constante universal de la gravedad, en la cifra aiguiente:

G= 6,674 . 10¹¹ N . m²/ kg²  donde N es Newton, una unidad de medida de la fuerza, m es metro y kg , obviamente, kilogramo.

Ya se conoce, entonces el valor G, pero sigue en pie la incógnita relativa a la masa de la Tierra. Ése fue el paso siguiente.

¿Qué determinación siguió luego?

Ahora con la constante G medida, sólo se requiere reemplazar una de las masas del sistema de medición, por la masa de la Tierra misma. Ni pensar en colgarla del aparejo, de modo que simplemente, lo que se hace es permitir la acción de la gravedad terrestre, colgando una masa conocida m, de un resorte vertical, (Figura 1) que le permite «caer» tanto como sea atraída por la masa terrestre. El resorte tiene un módulo de deformación (por estiramiento) conocido, que representa la fuerza ejercida por la interacción de las masas m del explorador y M de la Tierra, y modificada por la distania que las separa. Otra vez la formulita.

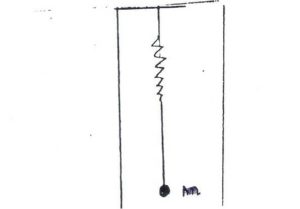
Figura 1.

En este caso, se conoce m de antemano, F se deduce del estiramiento del resorte, G, es constante y ya medida, y r es el radio de la Tierra, más la altura del punto del que pende la masa m. Resolviemdo la fórmula se midió por fin la masa de la Tierra.

¿Qué resultados se obtuvieron?

Las primeras mediciones estimaron una masa aproximada de unos 5.876 trillones de toneladas y una densidad de 5,48 g /cm³. Posteriormente, Poynting, en 1878, refinó un tanto la construcción del aparato, pero sólo logró una mínima corrección, estableciendo la densidad en 5,49 g /cm³.

¿Cómo evolucionó luego ese conocimiento?

Hubo numerosas correcciones desde entonces, que nunca se alejaron demasiado de los resultados arrojados por el experimento original. No fue sino hasta la segunda mitad del S XX, que se dieron a conocer valores más precisos, en función de los datos obtenidos a partir de los lanzamientos de satélites artificiales, cuando la observación de las desviaciones en sus trayectorias, por efectos de la gravedad terrestre, abrió un nuevo campo de experimentación. Los valores promedio que se aceptan hoy son de 5,98 . 10²⁷ g para la masa, y  5, 517 g /cm³ para la densidad.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La imagen que ilustra el post es de «Fundamentos de Geomorfología» de Rice, ligeramente modificada por mí.

Este apunte tiene sus años, pero sigue vigente y puede ser de utilidad para los alumnos de las materias relacionadas con el suelo, tanto en Geología como en Agronomía y diversas Ingenierías.

Deben leerlo a través del sistema Scribd, donde lo pueden descargar también.

ESTRUCTU_ by Graciela L. Argüello on Scribd

No hace mucho, introduje ya el concepto de perfil de equilibrio, y les adelanté que era un concepto teórico, y que en la práctica, ese perfil ideal nunca se alcanza de modo duradero- y mucho menos permanente- porque cualquier mínimo cambio lo altera por completo, ya que se trata de un sistema complejo.

Después de repasar el post, he tenido la sensación de que podemos explicitar un poco más ese tema, y a eso voy a dedicar el texto de hoy. Por supuesto, les orde sugiero amablemente que vayan a leer ese post anterior antes de internarse en éste.

¿Qué conceptos conviene introducir para comprender mejor el tema?

Para que todo lo que sigue nos quede definitivamente claro, debemos conocer al menos los conceptos de potencia neta y potencia bruta, y su efecto sobre la dinámica fluvial resultante.

¿Qué es la potencia bruta?

Comencemos poe decir que potencia es de modo general la capacidad de producir trabajo, y en el caso particular de un río, es su capacidad de cargar y transportar material.

La potencia de una corriente de agua es proporcional al caudal (masa de agua en movimiento), y al cuadrado de la velocidad con que discurre. Esto se expresa así:

P= Q x V²  donde P= potencia; Q= caudal y V= velocidad.

A su vez, el caudal se obtiene matemáticamente al multiplicar la superficie total de una sección transversal del área mojada por la corriente (S), por la velocidad con que corre (V). La razón de esta fórmula es obvia: imaginen un caño, cuanto más grande sea el diámetro (y por ende la superficie de la sección) y más rápido pase el agua por él, más cantidad (caudal) pasa.

Q= S x V, si reemplazamos Q en la fórmula anterior resulta:

P= S x V x V² que en definitiva es igual a  P= S x V³

Ya tenemos pues la fórmula de la potencia de una corriente. Pero no hay una única forma posible de considerar a la potencia. Lo que dijimos hasta aquí se conoce como potencia bruta, cuando aplicamos un sentido estricto. En definitiva, se trata de la capacidad de transporte y carga disponible en un sistema ideal y supuestamente invariable.

¿Qué es la potencia neta?

Cuando hacemos un análisis más realista del sistema fluvial, observamos de inmediato que siempre hay algo de carga en él, sean sedimentos, material biológico, o contaminantes. En definitiva, esa potencia bruta, que no es otra cosa que energía disponible teóricamente para el transporte, es en parte absorbida por los rozamientos que ocurren entre el agua y su carga, o por la reistencia que oponen la viscosidad, la rugosidad del lecho, etc.

El resto de capacidad de carga, que permanece cuando se resta la que se pierde como acabo de describir, es lo que se conoce como potencia neta.

En una fórmula aproximada:

Pn= Pb – (Par+ Patc) donde:

Pn= potencia neta

Pb= potencia bruta

Par= potencia absorbida por los rozamientos y rugosidad

Patc= potencia absorbida en el transporte de la carga

¿Cómo se relacionan ambas potencias entre sí, y cómo se manifiesta esa relación en los procesos fluviales?

Repitamos la fórmula que explicamos arriba:

Pn= Pb – (Par+ Patc)

Si el resultado es positivo, es decir que hay una potencia bruta superior a las pérdidas, la corriente tiene capacidad para adquirir más carga, erosionando el cauce, o recibiendo material aportado de otra forma.

Si el resultado es negativo, es decir que las pérdidas por rozamiento y carga superan a la potencia bruta, la corriente lo compensa, depositando algo de la carga, es decir que ocurre sedimentación en ese punto del curso.

Cuando el resultado es cero, en cambio, vale decir que las pérdidas de energía y la potencia bruta se igualan, entonces no ocurre erosión ni sedimentación. Sería la definición del perfil de equilibrio.

En otras palabras, el perfil de equilibrio es aquél a lo largo del cual, se mantiene una potencia neta igual a cero, porque las pérdidas son siempre equivalentes a la potencia bruta.

¿Qué sucede a lo largo del perfil de equilibrio?

Lo que dijimos al final de la respuesta anterior es inviable en la naturaleza. Jamás podrá mantenerse el valor cero de la Potencia neta a lo largo de todo el perfil; y ni siquiera por mucho tiempo en un único punto del perfil.

Esto sucede porque todos los puntos del perfil son interdependientes, y si por alguna razón la potencia cambia en un punto, todos los demás se reajustan a su vez.

Supongamos un perfil con potencia neta igual a cero. ¿Cuánto tardará en ocurrir una lluvia que aumente el caudal, y por consiguiente cambie la potencia bruta, que al aumentar también dejará un resto de energía para socavar el cauce? ¿O a la inversa, cuánto pasará hasta que caiga más carga desde las laderas, o alguien tire algo, aumentando el rozamiento, y disminuyendo la potencia bruta, hasta el punto en que dispare la sedimentación en ese lugar del curso?

Esto en un recodo dado del río. Pero si en un punto ocurre erosión, en otro, ese material cargado por el propio socavamiento, se hará excesivo y se depositará algo de material en otro punto. Esto explica la continua variación del perfil de equilibrio, que por eso mismo se convierte en un concepto de referencia meramente teórico.

Y a todo esto se debe sumar lo que ya les expliqué de los cambios de nivel de base, que inciden en la configuración del perfil tanto real como de equilibrio.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La foto que ilustra el post es del Tigre, lugar que me encanta.

Aquí comparto con ustedes el enlace a un video muy divertido pero muy didáctico también.

No dejen de verlo.

Como este post es continuación del de la semana anterior, en caso de que no lo hayan hecho ya, les recomiendo ir a leer la primera parte, antes de internarse en ésta de hoy.

La semana pasada contesté las siguientes preguntas:

¿Cómo armar la ficha de reconocimiento mineral?

¿Cómo reconocer cada propiedad de las mencionadas?

Hoy continuaremos desde aquí.

¿Cómo determinar un mineral, a partir de la ficha de observación?

Una vez que se ha completado la ficha, tal como lo he explicado en la primera parte de este tema la semana pasada, se entra con los datos a una tabla que a partir de las propiedades encontradas, conduce al nombre del mineral en cuestión. Obviamente es aquél en el que coinciden todas las que figuran en la tabla con las que se han reunido en la ficha del ejemplar que se ha analizado.

¿De qué tabla se trata la que aquí se presenta? ¿Hay otras?

Hay numerosos atlas, libros y tablas para esta determinación, muchos de los cuales se encuentran inclusive en Internet, pero algunos son muy complicados o incluyen propiedades que no se determinan macroscópicamente, o caracteres químicos que se reconocen con análisis de laboratorio.

Por esa razón, he escaneado para ustedes una tabla muy vieja, como verán en la portada, pero que creo que es de todas las que conozco, la de manejo más sencillo para quienes no tienen una preparación específica en Mineralogía, además de ser lo bastante corta como para permitirme este escaneo.

Hay una aclaración que debo hacerles: aun en esta tabla que es tan sencilla, van a encontrar en la columna de clivaje un código numérico que casi seguramente no entenderán, al menos por ahora, porque se refiere a la posición en el espacio, del plano de ruptura. Para comprender el código deberían tener mucho más conocimiento sobre cristalografía, pero eso les llevará tiempo. Tengan paciencia.

Y la última aclaración: la buena determinación del mineral depende totalmente de la corrección con la que hayan definido sus propiedades.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La foto que ilustra el post fue tomada por el Pulpo en uno de sus viajes a USA, y está subida en este sitio.