Locos por la Geología

Archivo de la categoría ‘Geología para principiantes’

Como este post es continuación del de la semana anterior, en caso de que no lo hayan hecho ya, les recomiendo ir a leer la primera parte, antes de internarse en ésta de hoy.

La semana pasada contesté las siguientes preguntas:

¿Cómo y cuándo surgen estos conceptos?

¿Cuál es el concepto N° 1?

¿Cuál es el concepto N° 2?

¿Cuál es elconcepto N° 3?

¿Cuál es el concepto N° 4?

Desde aquí, seguiremos contestando las siguientes preguntas:

¿Cuál es el concepto N° 5?

Comienzo transcribiendo lo que expresó Thornbury.

En la evolución geomórfica la complejidad es más común que la simplicidad.

Como ya he señalado antes muchas veces, los sistemas naturales, por ser tan abiertos e intercomunicados, adquieren una gran complejidad. De allí que los paisajes resultantes tengan también historias donde lo simple es escaso, y resulta más bien de la falta de comprensión, o de la esquematización intencional por parte del hombre que intenta leerla.

Sin embargo, tampoco lo simple es inexistente en el relieve, de allí que se haya generado una clasificación de los paisajes que les presento a continuación:

• Paisajes sencillos: Son los que responden a un solo proceso geomorfológico. En un sentido muy estricto, casi ninguno lo es, salvo el caso de una colada de lava reciente, en la que todo el paisaje queda cubierto por ella, y no se visualizan rasgos de ningún otro origen; o tal vez en el de una corriente de lodo- también reciente- que genera una situación comparable a la mencionada. No obstante, cuando se da a la expresión «paisaje sencillo» en un sentido más amplio, pueden incluirse bajo esa designación aquellos relieves donde hay un solo proceso claramente dominante, aunque no llegue a ser excluyente. Es el caso de las dunas eólicas, las planicies fluviales, o los acantilados marinos, donde el viento, los ríos o el mar respectivamente son los causantes principales de las formas visibles.
• Paisajes compuestos: Son, en cambio, los que responden a la acción conjunta de varios procesos, y constituyen la gran mayoría de las topografías que se observan en una región dada. En ella accionan simultáneamente diversos procesos, como meteorización física y química, acción del viento, de los organismos, del agua corriente, etc.
• Paisaje monocíclico: Un paisaje, ya sea sencillo o compuesto, puede ser la respuesta a un único ciclo o a la sucesión de varios ciclos, separados por crisis tectónicas, climáticas, o eustáticas. En el primero de los casos, estamos ante los denominados paisajes monocíclicos. Si se trata de paisajes sencillos relacionados con el vulcanismo, la construcción del relieve se debe a una sola efusión. Si se trata de paisajes compuestos, todos los procesos se produjeron de manera continuada, sin interrupciones significativas.
• Paisaje policíclico: Se trata de los paisajes que sí han sufrido interrupciones causadas por las crisis mencionadas en el punto anterior. También en este caso, la policiclicidad puede afectar a paisajes sencillos o a paisajes compuestos. Supongamos, como ejemplo un paisaje sencillo compuesto solamente por lavas; si ellas corresponden a diversos pulsos de emisión, se formarán de todos modos paisajes policíclicos, sin que dejen de ser sencillos. En el caso de los paisajes compuestos, también todo el conjunto de procesos puede ser interrumpido por las crisis que ya hemos mencionado; y generar luego formas diferentes, sobreimpuestas a las anteriormente producidas.
• Paisaje resurrecto o exhumado: Se trata de paisajes policíclicos, naturalmente, pero pueden ser sencillos o complejos. Sea cual haya sido su historia pasada, resultan enterrados por alguna cubierta, que puede ser sedimentológica, de suelos, de glaciares, o bien de lavas. Pasado un largo intervalo, los rasgos de esa topografía vuelven a aparecer en superficie cuando la erosión, la acción antrópica, el tectonismo, o una combinación de todas esas acciones remueven la cubierta, y «desentierran» el relieve antiguo.

¿Cuál es el concepto N° 6?

La transcripción del texto de Thornbury es:

La mayor parte de la topografía de la Tierra tiene una edad que no va más allá del Pleistoceno, mientras que es exigua la topografía anterior al Terciario.

Después de haber leído lo anterior, ya les quedará claro que los paisajes que hoy vemos tienen historias con tantas alternativas que no pueden tener una larga permanencia sin que evolucionen a topografías totalmente diferentes. Recuerden que la Topografía se refiere solamente a la expresión superficial del relieve. No se está haciendo alusión a la Geología de la zona de que se trate.

¿Cuál es el concepto N° 7?

Comienzo con el texto de Thornbury:

La interpretación cabal de los paisajes actuales es imposible sin una apreciación total de las influencias múltiples de los cambios geológicos y climáticos ocurridos durante el Pleistoceno.

Hoy la parte que no convalidamos es la que le pone un límite temporal a las influencias geológicas y climáticas que se deben tener en cuenta al interpretar un paisaje. Cambios mucho más antiguos que los del Cuaternario son también partícipes de las geoformas resultantes. Si eliminamos las palabras «durante el Pleistoceno», el concepto conserva toda su vigencia, según seguiremos viendo en numerosos posts todavía por venir.

¿Cuál es el concepto N° 8?

Thornbury escribió en su momento:

Para comprender cabalmente la importancia variada de los diferentes procesos geomórficos es necesaria una apreciación de los climas del mundo.

No se dejen confundir por el parecido entre las formulaciones de este concepto y el anterior. En el N° 7 se hace referencia a cambios temporales de los climas, aquí en cambio se apunta a los cambios espaciales, es decir a la distribución climática en el planeta. Sobre este punto volveremos al hablar de los Dominios morfoclimáticos en un post futuro.

¿Cuál es el concepto N° 9?

Lo que dijo al respecto Thornbury fue:

Aunque el interés primario de la Geomorfología son los paisajes actuales, su utilidad máxima la logra por extensión histórica.

Ya al presentarles el Concepto N° 1,  (el lunes pasado) les sugerí ir a leer el post sobre la Ley del Actualismo, formulada por Hutton. En ese post les expliqué el interés de extender ese principio tanto hacia atrás como hacia adelante en la historia. Eso que escribí entonces, explica este concepto. Si no lo han hecho ya, les sugiero ir a leerlo ahora.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La foto que ilustra el post es de la Polinesia Francesa.

Si bien estos conceptos fueron planteados hace ya muy muchos años, tienen todavía bastante vigencia, sobre todo cuando se los revisa y actualiza a la luz de nuevas concepciones. Pero como aun para refutarlos es necesario conocerlos, me parece interesante presentarlos aquí, con algunos primeros comentarios, que iremos profundizando a lo largo de nuestros encuentros.

Como este tema se vuelve extenso, lo dividiré en dos posts, el primero de los cuales es el de hoy, y el segundo aparecerá el próximo lunes.

¿Cómo y cuándo surgen estos conceptos?

Estos conceptos fueron enunciados en Principles of Geomorphology, de William Thornbury hacia finales de la década de 1950, y de allí los he tomado para resumirlos y comentarlos aquí.

¿Cuál es el concepto N° 1?

Este concepto se expresa en el texto de Thornbury de la siguiente forma:

Los mismos procesos y leyes físicas que actúan hoy en día, actuaron a través de todo el tiempo geológico, aunque no necesariamente siempre con la misma intensidad del presente.

Si ustedes son lectores constantes del blog, reconocerán que este principio no es otro que la ley de Hutton, conocido como actualismo, o de las causas actuales, y sobre el cual ya he escrito un post, donde inclusive presenté las críticas y su actualización, de modo que no haré aquí más que remitirlos a ese mismo post.

¿Cuál es el concepto N° 2?

Copio primero el texto de Thornbury:

La estructura geológica es un factor dominante de control en la evolución de las formas del relieve, y se refleja en ellas.

Para entender este concepto, es importante hacer notar que aquí el término estructura se está empleando en el sentido má¡s amplio, es decir que no incluye solamente los rasgos estructurales de oigen tectónico, como las fracturas o pliegues, sino también otras características, tales como la forma de depositación de materiales, si hay o no estratificación, las características litológicas, y la exposición de las rocas a los agentes del clima, es decir si están en umbrías o solanas, a barlovento o sotavento, entre muchos otros detalles.

Todo eso que mencionamos arriba, y que ahora sabemos que el término «estructura» comprende cuando se lo aplica en Geomorfología; es casi siempre anterior a las formas del relieve que se pueden observar en la actualidad, y es definitorio en el curso de los procesos exógenos que las han modelado y las continúan modificando.

Por eso es imprescindible reconocer la estructura geológica, antes de describir y analizar las geoformas presentes en un paisaje cualquiera.

A veces la influencia de la estructura es medianamente obvia- como cuando un pliegue tectónico se manifiesta con una lomada en superficie- pero cuando no lo es, también debe buscarse, porque siempre existe, aunque a veces llega a ser precisamente lo opuesto de lo que podría ingenuamente esperarse, como veremos alguna vez en posts en los que hablaremos de inversiones del relieve original.

¿Cuál es el concepto N° 3?

La cita correspondiente en el texto de Thornbury es:

Los procesos geomórficos dejan su impresión distintiva sobre las formas del terreno y cada proceso geomórfico desarrolla su propio conjunto de formas distintivas.

Esto, que parece una verdad de perogrullo en nuestos días, en su momento fue novedoso y revolucionó la interpretación del paisaje. Hoy todos sabemos que las dunas responden esencialmente a un proceso eólico, y las cárcavas a su vez, a dinámicas pluviales como principales modeladoras. Aunque por supuesto- cosa que repetiremos en otro concepto, y ya hemos visto en otro post- los procesos no actúan de manera exclusiva ni excluyente en ningún relieve.

Cada proceso, en definitiva, deja su sello reconocible, en un paisaje dado, pero no es más que el principal protagonista de un «elenco» complejo en el que participan otros actores más.

Por otra parte, hay también que tener en cuenta que a veces procesos diferentes pueden dar por resultado, formas semejantes entre sí. Ese fenómeno es la equifinalidad que expliqué en el post que he linkeado más arriba. De allí que la validez de este concepto N° 3, no es tan absoluta como podría creerse, y por eso es que en mis explicaciones he incluido expresiones como «esencialmente», o «principales modeladoras». Nunca debemos pensar de maneras inflexibles en la comprensión de un relieve. En todo cso, es más importante analizar un conjunto de formas que una única geoforma aislada del contexto.

¿Cuál es el concepto N° 4?

El texto de Thornbury lo manifiesta de esta forma:

A medida que los diferentes agentes erosivos actúan sobre la superficie terrestre, se produce una secuencia en las formas del relieve, con características en los sucesivos estados de su desarrollo.

Éste es sin duda el concepto más cuestionado y cuestionable, puesto que la evolución del paisaje ya no se considera como resultante de un camino tendido hacia adelante, y que se recorre en la misma dirección y sentido a lo largo del tiempo. Hoy sabemos que hay avances y retrocesos, complicaciones y cambios rápidos, resultantes de determinadas situaciones críticas. Algo de esto lo he adelantado un poco, al hablar de biostasia y rexistasia.

En el momento en que se formuló este concepto N° 4, era aceptada en todos sus puntos la Teoría de Ciclos de Davis, que hoy ha sido superada, aunque la utilidad de las etapas que él planteaba, no se discute a los fines descriptivos. Hoy ya no las consideramos como «etapas», lo que tiene una connotación temporal; sino como «estados», que simplemente caracterizan un momento dado.

Pero este punto, que nos remite a algo tan interesante como el nacimiento, crítica y evolución de la Teoría de ciclos de Davis, amerita un post que haré más adelante. Lo de hoy es solamente un aperitivo. Ya van a probar el plato principal en el futuro.

Hasta aquí llegamos hoy, la semana que viene seguiremos contestando las siguientes preguntas:

¿Cuál es el concepto N° 5?

¿Cuál es el concepto N° 6?

¿Cuál es el concepto N° 7?

¿Cuál es el concepto N° 8?

¿Cuál es el concepto N° 9?

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La foto que ilustra el post es de la meseta central estadounidense.

Ya hemos hablado de varios temas relativos a la dinámica fluvial, y es un buen momento para explicar algunos principios físico- matemáticos que rigen el transporte y la sedimentación de las partículas transportadas por un fluido en movimiento.

Y digo un fluido y no el agua, porque son igualmente válidos para el movimiento del aire, es decir el viento, cambiando solamente algunos valores numéricos en los ejes X e Y.

Lo que les presento entonces hoy es la Curva de Hjulström, que complementaré más tarde con la ley de Stokes, en otro post.

¿Quién fue Hjulström?

Filip Hjulström nació en Suecia el 6 de octubre de 1902, y se hizo mundialmente conocido por la publicación de su tesis doctoral titulada «The River Fyris» (el Río Fyris), en la que presentó uno de los primeros estudios cuantitativos sobre procesos geomorfológicos de que se guarda registro.

Posteriormente, en conjunto con sus alumnos, continuó estudios de tal importancia, que llegaron a constituir la Escuela Upsala de Geografía Física. Hjulström falleció en 1982, dejando un importante legado científico, y sin haberlo sospechado nunca, también artístico.

En efecto (y esto lo agrego como nota de color), Filip Hjulström, fue el padre de Lennart Hjulström, que se convertiría en un notable actor sueco, casado con la también actriz Ulla Söderdal, con quien tendría dos hijos que también se dedicaron a la actuación: Niklas y Carin Hjulström.

¿Qué es la curva de Hjulström?

La curva de Hjulström es un diagrama de uso muy extendido en la Geomorfología, que describe los umbrales que en función de los cambios de velocidad de una corriente, definen si hay arranque, transporte o sedimentación. para cada tamaño de partícula involucrada en el proceso.

¿Cómo se entiende la curva de Hjulström?

Como siempre he dicho a mis alumnos, para comprender un diagrama cualquiera, lo primero a hacer es observarlo. Ver en detalle qué partes lo conforman, qué unidades de medida están involucradas, y cómo se comportan las curvas, barras o campos resultantes. Hagámoslo así, pues.

¿Qué rasgos se destacan en la curva?

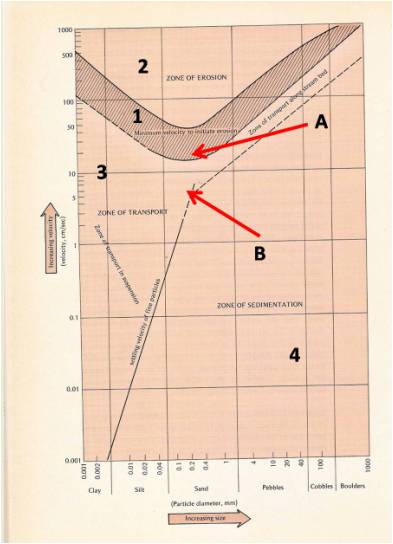
Se trata de un sistema de ejes XY, compuesto por los siguientes elementos:

• En el eje X (abcisas), se observan los diversos tamaños de partículas presentes en el curso del río en este caso, aunque podría aplicarse (cambiando sólo los valores aritméticos) a fenómenos eólicos, es decir corrientes de aire. Sobre las abcisas, los tamaños crecen desde la intersección de los dos ejes, hacia la derecha, y se miden en mm. Allí aparecen intervalos de tamaños que corresponden sucesivamente a las arcillas, limos, arenas, guijas, guijarros y guijones.
• El eje Y (ordenadas) implica el crecimiento hacia arriba de la velocidad del fluido en movimiento, y la unidad es m/segundo.
• Ya en el interior del diagrama, se observan las curvas que conectan todos los puntos críticos en que las partículas de cada tamaño, pasan de una situación a otra diferente, ya sea de reposo a arranque, de arranque a transporte o de transporte a sedimentación. En un caso se trata de curvas literalmente, y en otro caso se trata de dos segmentos rectos, que de todos modos se designan como curva.
• Esas curvas que mencionamos arriba, separan distintos campos, a saber: zona de erosión (propiamente dicha, o arranque del material), que les he marcado con un 2 en el gráfico; zona de transporte, que marqué con 3; y la zona 4, que es la de sedimentación o depósito. La zona 2 o de arranque, está en la porción más alta del gráfico porque es la que requiere mayor velocidad. Una vez puesta en movimiento la partícula, la energía necesaria para mantenerla en tránsito puede ser menor, porque la propia inercia juega a su favor.
• La zona que les indiqué con 1, es un intervalo que incluye las velocidades mínimas que se requieren para que los materiales de cada tamaño sean arrancados del cauce, sea del lecho o de las riberas. Es una zona y no una sola línea, porque hay numerosos factores que la afectan, como por ejemplo, la turbulencia, la carga que ya transporta el agua y que modifica su potencia neta, etc.
• Por arriba del punto B, la zona de transporte implica un arrastre de materiales gruesos por el fondo del lecho, mientras que hacia abajo de ese punto, siendo menor la velocidad, se transportan partículas finas por otros mecanismos, como flotación, rodamiento, saltación, y más abajo aún, (es decir con menos velocidad) por suspensión.

¿Por qué desciende la curva en el punto A?

Figura 1. La cohesión de las arcillas.

La lógica indica que cuanto más pequeña es la partícula, menor es la velocidad requerida para el arranque y puesta en movimiento.

Esto nos haría pensar que la curva debería ser siempre ascendente hacia la derecha donde se encuentran los tamaños más gruesos, y sin embargo, hay una menor velocidad crítica en ese punto A, que corresponde al tamaño de los limos.

Eso ocurre porque las partículas más finas que el limo, tienen una fuerza de cohesión que debe ser vencida para el arranque, que no aparece en cambio en el limo y las demás partículas. Por eso, en el extremo de la izquierda, donde están las partículas de arcilla, se necesita más velocidad para la erosión ss, y la curva sube.

La explicación está en la característica micelar de las arcillas que por diversas razones, tienen normalmente carga eléctrica negativa en sus bordes (Figura 1). Al estar inmersas las partículas en agua, o en presencia de humedad, las propias moléculas de agua- con sus cargas orientadas que constituyen dipolos eléctricos– actúan como aglutinantes de las micelas de arcilla, al unir sus cargas positivas a los polos negativos de estas últimas.

¿Por qué cambia bruscamente la pendiente de la curva en el punto B?

Porque hacia la derecha, el tamaño tan grande de los materiales involucrados, requiere una gran energía para el transporte, y un mínimo descenso en la velocidad del flujo pasa los cuerpos transportados de ese campo, al de la sedimentación, en otras palabras, se depositan rápidamente.

Traducido: para una amplio rango de tamaños, hay ligeros cambios de velocidad crítica para el depósito, por eso, la curva se horizontaliza comparativamente. Hacia la izquierda ocurre exactamente lo inverso. La curva se empina porque se necesitan grandes cambios de velocidad sobre el eje Y, para que los tamaños decrecientes de partículas resulten depositadas, pues muchas de ellas pueden incluso permanecer en suspensión con velocidades próximas al cero.

Pero eso ya lo describe la ley de Stokes que veremos en otro post.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La imagen que ilustra el post es una modificación personal sobre la figura que aparece en el libro The Evolving Earth, de Sawkins.

Para poder seguir avanzando en el reconocimiento de las medidas de nuestro planeta, es importante que repasen dos posts anteriores, o más propiamente dicho, un post en dos entregas.

En la primera parte, les expliqué la Ley de la Gravitación Universal, que será la base teórica de lo que analizaremos hoy, y sin la cual no entenderán nada. En la segunda, les adelanté una descripción muy general del experimento con que se «pesó» la Tierra, y que prometí aclarar en detalle más adelante, que es precisamente lo que me dispongo a hacer ahora.

¿Con qué datos se contaba antes de esta medición?

Como habrán visto en los posts que les mandé a leer, se tenía clara la fórmula de la gravedad universal, donde figuraba la Constante de la Gravedad, pero ésta era desconocida hasta la experiencia que hoy nos ocupa.

Por otra parte, ya desde muchos siglos antes se conocía la longitud del arco de meridiano, gracias a la determinación de Eratóstenes que les conté en este otro post .

Conocer la longitud del arco de meridiano permitió a su vez definir la circunferencia de la Tierra, según las inferencias que les mostré en la parte 1 del post que he linkeado más arriba.

Ahora bien, una vez que se conoce el perímetro de la circunferencia, sólo es cuestión de aplicar un par de fórmulas básicas y sencillas de la Geometría para obtener datos que necesitamos para «pesar» la Tierra.

Sabemos que el perímetro de la circunferencia (Pc) es:

Pc= π . d

donde π es pi, de valor conocido; y d es el diámetro (o dos veces el radio) de la Tierra, que buscamos conocer. Despejando pues en la fórmula, resulta:

d= Pc/ π

Y una vez que se ha calculado el radio r (que es la mitad del diámetro), sólo hay que usarlo en la fórmula del volumen de la esfera (Ve).

Ve= 4/3 π . r³

El volumen resultante al aplicar la fórmula con los valores del planeta, fue de 1,0842 x 10⁸ km³. Por supuesto que se trata de un volumen sólo aproximado, porque, como también les he explicado, la Tierra dista mucho de ser una simple pelota. Más bien se da el lujo de tener una forma propia a la que llamamos geoide, pero cuyo volumen podemos a través de esa fórmula medianamente estimar. Y todavía hacemos otra concesión, ya que en lo que sigue, pensaremos el volumen como equivalente a la masa, porque en cierta medida lo es.

Aδun con todas estas dispensas, ya contamos con una parte de los datos que requerimos para conocer la densidad (δ) de la Tierra. Como sabemos que densidad es el cociente entre la masa y el volumen, bastará con determinar la masa para conocer su densidad según la fórmula:

δ= M/V

donde δ es densidad; M es masa y V es volumen.

¿En qué consiste el experimento de Cavendish?

Ya les dije en uno de los posts que les mandé a leer, que el experimento con el que se pretendió «pesar la Tierra» fue ideado por Lord Cavendish en 1798, en su casa de Clapham Common. En los hechos, no fue la masa de la Tierra lo que determinó en realidad con ese experimento, sino el valor de la constante Universal de la Gravedad (G), pero una vez que se conoció ésta, el paso siguiente fue muy sencillo, y ya pudo conocerse el valor de la masa terrestre agregando sólo un datito más.

El punto de partida es la fórmula de F que es la fuerza de atracción gravitacional.

F= G. m.m’ / r²

Recordemos que F es la fuerza de atracción que se ejerce siempre entre dos cuerpos cualquiera.

m es la masa de uno de los cuerpos sometidos a esa fuerza.

m’ es la masa del otro cuerpo.

r es la distancia que separa ambos cuerpos.

Ahora veamos la construcción de la balanza de Cavendish, que es la que se ve en la ilustración superior. Este aparato consta de dos masas m y m’ , cada una de las cuales está a su vez dividida en dos esferas de plomo, pequeñas en el caso de m, y grandes en el caso de m’, pero todas de valor conocido.

Las dos bolas que forman la masa m están suspendidas de una estructura que al impedirles caer, las independiza de la atracción gravitacional terrestre, y las hace en cambio dependientes en su movimiento, sólo de la atracción gravitacional ejercida por las otras dos esferas que suman la masa m’. Éstas, a su vez, están sustentadas sobre un plato que les permite girar pero no caerse.

En definitiva, las esferitas solamente pueden girar alrededor de los ejes de los aparejos que las sostienen, y lo hacen en respuesta a la fuerza gravitatoria F que se genera entre ambas masas m y m’. Obviamente, esa fuerza responde a la fórmula general de la gravedad ya repasda más arriba.

Como los detalles de construcción del aparato son todos conocidos, se sabe de antemano cuál es el valor de las masas m y m’, y también el del radio r que las separa. Para conocer G, hay que medir F y resolver la ecuación, que ahora pasará a ser:

G= F. r² / m.m’

Cavendish resolvió el problema de manera sencilla: el cable del cual penden las esferas que constituyen la masa m tiene un módulo de torsión conocido, es decir que gira un cierto ángulo bien determinado por cada unidad de fuerza aplicada. Estableciendo cuánto ha rotado el hilo se mide pues F. Ésa es la función del espejo solidario con el cable, y que a medida que más se tuerce éste, va reflejando la luz incidente sobre él, en una porción más alejada de la inicial, que se toma como cero, en la escala graduada.

Con todos los valores ya conocidos, se pudo establecer la constante universal de la gravedad, en la cifra aiguiente:

G= 6,674 . 10¹¹ N . m²/ kg²  donde N es Newton, una unidad de medida de la fuerza, m es metro y kg , obviamente, kilogramo.

Ya se conoce, entonces el valor G, pero sigue en pie la incógnita relativa a la masa de la Tierra. Ése fue el paso siguiente.

¿Qué determinación siguió luego?

Ahora con la constante G medida, sólo se requiere reemplazar una de las masas del sistema de medición, por la masa de la Tierra misma. Ni pensar en colgarla del aparejo, de modo que simplemente, lo que se hace es permitir la acción de la gravedad terrestre, colgando una masa conocida m, de un resorte vertical, (Figura 1) que le permite «caer» tanto como sea atraída por la masa terrestre. El resorte tiene un módulo de deformación (por estiramiento) conocido, que representa la fuerza ejercida por la interacción de las masas m del explorador y M de la Tierra, y modificada por la distania que las separa. Otra vez la formulita.

Figura 1.

En este caso, se conoce m de antemano, F se deduce del estiramiento del resorte, G, es constante y ya medida, y r es el radio de la Tierra, más la altura del punto del que pende la masa m. Resolviemdo la fórmula se midió por fin la masa de la Tierra.

¿Qué resultados se obtuvieron?

Las primeras mediciones estimaron una masa aproximada de unos 5.876 trillones de toneladas y una densidad de 5,48 g /cm³. Posteriormente, Poynting, en 1878, refinó un tanto la construcción del aparato, pero sólo logró una mínima corrección, estableciendo la densidad en 5,49 g /cm³.

¿Cómo evolucionó luego ese conocimiento?

Hubo numerosas correcciones desde entonces, que nunca se alejaron demasiado de los resultados arrojados por el experimento original. No fue sino hasta la segunda mitad del S XX, que se dieron a conocer valores más precisos, en función de los datos obtenidos a partir de los lanzamientos de satélites artificiales, cuando la observación de las desviaciones en sus trayectorias, por efectos de la gravedad terrestre, abrió un nuevo campo de experimentación. Los valores promedio que se aceptan hoy son de 5,98 . 10²⁷ g para la masa, y  5, 517 g /cm³ para la densidad.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La imagen que ilustra el post es de «Fundamentos de Geomorfología» de Rice, ligeramente modificada por mí.

Este apunte tiene sus años, pero sigue vigente y puede ser de utilidad para los alumnos de las materias relacionadas con el suelo, tanto en Geología como en Agronomía y diversas Ingenierías.

Deben leerlo a través del sistema Scribd, donde lo pueden descargar también.

ESTRUCTU_ by Graciela L. Argüello on Scribd