Mark Twain and Ecology (En castellano el próximo viernes)
 In his book «The American Claimant» (published in 1892) Mark Twain (Sam Clemens)- also the author of Tom Sawyer’s Adventures and many other wonderful novels- seems to be far ahead his time.
In his book «The American Claimant» (published in 1892) Mark Twain (Sam Clemens)- also the author of Tom Sawyer’s Adventures and many other wonderful novels- seems to be far ahead his time.
Being Twain a humorist it is not easy to say wether the whole idea was considered by him as a possibility or just as other of his absurd jokes.
Anyway, the following paragraph might be considered as an early ecological proposal. Just read it:
…everything is useful- nothing ought ever to be wasted. Now look at sewer gas, for instance. Sewer gas has always been wasted, heretofore; noboby tried to save up sewer- gas–you can´t name a man. Ain’t that so? you know perfectly well it´s so…
…Do you see this little invention here?–it’s a decomposer- I call it a decomposer. I give you my word of honor that if you show me a house that produces a given quantity of sewer- gas in a day, I’ll engage to set up my decomposer there and make that house produce a hundred times that quantity of sewer-gas in less than half an hour…
…for iluminating purposes and economy combined, there’s nothing in the world that begins with sewer gas. And really it don’t cost a cent. You put in a good inferior article of plumbing -such as you find everywhere- and add my decomposer, and there you are. Just use the ordinary pipes- and there yor expenses ends. ..
…in five years from now you won’t see a house lighted with anything but sewer-gas…
Los tehuelches y su visión del cosmos.
 Estando en vísperas de las vacaciones de invierno, me pareció que se imponía un post desacartonado y pintoresco, lo que me llevó a elegir este tema, relacionado con las creencias de los antiguos pobladores de la pampa argentina.
Estando en vísperas de las vacaciones de invierno, me pareció que se imponía un post desacartonado y pintoresco, lo que me llevó a elegir este tema, relacionado con las creencias de los antiguos pobladores de la pampa argentina.
Ellos, como todos los antiguos pueblos, intentaron dar explicación a los fenómenos que los asombraban y deseaban comprender.
A diferencia del panteísmo propio de otras grandes civilizaciones,- es decir la tendencia a dotar de poderes divinos a todos los elementos y fenómenos de difícil explicación- los tehuelches relacionaron los procesos que observaban, con elementos de su vida cotidiana.
Su tendencia era pues, más irreverente, pero también más natural.
¿Cómo explicaban los tehuelches la Cruz del Sur?
Según los nativos, esa constelación era la huella de la pisada del ñandú cuando paseaba por el firmamento.
¿Cómo explicaban los tehuelches la visualización del planeta Marte?
Para ellos se trataba del carancho al acecho. Suponían que desde esas alturas se lanzaba en sus cacerías de pequeñas presas, como otras aves, roedores o reptiles.
¿Cómo explicaban los tehuelches la Vía Láctea?
Para los tehuelches, la Vía Láctea, era el resultado del polvo que levantaban los guanacos en sus migraciones y desplazamientos.
Si lo pensamos un poco, no es tan diferente de la explicación que daba la Iglesia Católica para la Galaxia a la que pertenecemos, ya que según su visión también se trataba del polvo que se producía por caminantes, en ese caso, humanos, tal como les expliqué en el post que les he linkeado más arriba.
¿Cómo explicaban los tehuelches las Nubes de Magallanes?
Para ellos, las nubes eran revolcaderos de guanacos, algo así como descansos especiales en su camino celeste.
¿Qué son las Nubes de Magallanes?
Las Nubes de Magallanes son dos galaxias enanas, pertenecientes al Grupo Local de galaxias, lo cual significa que están relativamente próximas, y hasta se verían afectadas en alguna medida por la Vía Láctea.
Las Nubes se distinguen entre sí por su tamaño, del que toman sus correspondientes nombres de Gran Nube de Magallanes y Pequeña Nube de Magallanes.
Si bien ambas se ven mejor desde el hemisferio austral en noches con cielo limpio y sin luna, los antiguos pueblos del Oriente Medio ya las conocían.
Fue el astrónomo persa Abd Al-Rahman Al Sufi quien las mencionó por primera vez en su Libro de las estrellas fijas, bautizándolas como Al Bakr (Buey Blanco). No obstante, el nombre con el que hoy se las conoce les fue dado en Europa, como homenaje a Fernando de Magallanes quien las observó durante su viaje de circunnavegación entre 1519 y 1522.
Las dos galaxias enanas están separadas entre sí por unos 21º, en la esfera celeste visible desde la Tierra, pero su distancia real es de unos 75.000 años luz.
Recordemos que la Vía Láctea es una galaxia en espiral, lo cual constituye la primera diferencia con las Nubes de Magallanes, que son irregulares, las otras diferencias residen en su masa significativamente menor, y su composición más rica en gas y más pobre en metales; y su población estelar muy joven.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente, porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.
P.S.: La imagen que ilustra el post la he tomado de Imágenes Google, que me direccionó a este sitio.
Más del artista Gustavo Bucalo.
 Ya les presenté hace un par de semanas a un artista que descubri aquí mismo, en Córdoba, exponiendo sus obras en la Alianza Francesa, y que me fascinó lo bastante como para pedirle que me dejara compartir con ustedes esta belleza, denominada Saurio. Se trata de una xilografía magistral, ¿no creen?
Ya les presenté hace un par de semanas a un artista que descubri aquí mismo, en Córdoba, exponiendo sus obras en la Alianza Francesa, y que me fascinó lo bastante como para pedirle que me dejara compartir con ustedes esta belleza, denominada Saurio. Se trata de una xilografía magistral, ¿no creen?
¿Qué le debe la Geología a Euclides, el matemático?
 ¿A qué Euclides nos referiremos aquí?
¿A qué Euclides nos referiremos aquí?
Empecemos por decir que el nombre original en griego se escribe Εὐκλείδης‚ y podría leerse Eukleides, y corresponde por lo menos a tres grandes personalidades históricas:
El Euclides conocido como «el Matemático» o «el Geómetra»-que es el que hoy nos convoca-; Euclides de Megara, cuyo campo de conocimiento es la Filosofía y que fue discípulo de Sócrates; y el que muchos siglos después se conocería como «el Euclides español», quien era en realidad el musulmán Abderramán Benismail, brillante geómetra que redactó un compendio de la obra aristotélica «Organon», y que mereció su apodo por el conocimiento matemático, que le obligó también a exiliarse por la persecución que se desató en su tiempo contra los estudiosos no ortodoxos.
Vuelvo pues a destacar que el nuestro de hoy es el Euclides matemático original.
¿Qué se sabe de la vida de Euclides?
No es mucho lo que de él se sabe, salvo que vivió aproximadamente entre los años 325 y 265 a. C. y que fue tal el legado que dejó tras de sí que se le conoce como «El Padre de la Geometría».
Sin embargo, sí puede asegurarse que siguiendo las sugerencias de Ptolomeo, fundó una Escuela de Matemáticas, en Alejandría- por ese entonces el centro del conocimiento y la sabiduría- y que generó tal devoción entre sus discípulos, que gran parte de su obra se conserva a través de las recopilaciones que ellos realizaron a partir de sus enseñanzas.
Hay dos hechos que pintan muy bien los rasgos sobresalientes de su personalidad y pensameinto.
Por una parte, tuvo la modestia de reconocer que no le era posible abarcar todo el saber existente, razón por la cual tomó el camino de la especialización, separando así las Matemáticas- en la que se consideraba más versado- del resto de la Filosofía, que por entonces pretendía resumir toda la sabiduría posible.
El otro hecho es una anécdota que se le atribuye, según la cual el rey Ptolomeo le preguntó si había una forma más fácil de acceder al conocimiento de la Geometría que la lectura de su libro Elementos, a lo cual Euclides (autor del libro en cuestión), respondió:
«No existe en Geometría ningún camino especial para los reyes».
¿Cuál fue su obra fundamental?
Según Heinrich Wieleitner, historiador científico de la primera mitad del S XX, la obra Elementos, de Euclides (completada con la recopilación de sus discípulos) es, luego de la Biblia y el Quijote, la más leída de todos los tiempos. Por supuesto esta afirmación debe tomarse en el contexto de la época en que se enunció, que fue mucho antes de la era de los best sellers.
También Carl Boyer dijo de Euclides, en 1956, que su obra fue la más ampliamente difundida de todos los tiempos, en el campo de la matemática, y le atribuye el mayor mérito a su formulación lógica de muchos conceptos (algunos ya existentes sobre todo en las escuelas de Eudoxio y Teaitetos), que supo organizar de manera impecable.
Elementos incluye XIII Libros, que a su vez sistematizan numerosas Proposiciones, Definiciones, Postulados y Nociones comunes.
Así , por ejemplo, el Libro I contiene 48 proposiciones, 23 definiciones, 5 postulados y 5 nociones comunes.
Las 48 proposiciones se pueden dividir en tres bloques, a saber: las primeras 26 tratan de las propiedades de los triángulos. Las siguientes seis establecen la teoría de las paralelas y demuestran que la suma de los ángulos de un triángulo suman lo mismo que dos ángulos rectos. Las restantes se refieren a los paralelogramos, triángulos, cuadrados, al Teorema de Pitágoras y a su inverso.
El Libro II se dirige al Álgebra geométrica, tiene 2 Definiciones y 14 Proposiciones
El Libro III alude a la Teoría de la circunferencia, con 11 definiciones y 37 proposiciones, 5 de las cuales son problemas y las otras teoremas.
El Libro IV atañe a las Figuras inscritas y circunscritas y consta de 7 definiciones y 16 proposiciones.
El Libro V incluye la Teoría de las proporciones abstractas, y en él se resuelve el problema planteado por el descubrimiento pitagórico de los números irracionales. Tiene 18 definiciones y 25 Proposiciones
El Libro VI trata sobre Figuras geométricas semejantes y proporcionales. Aquí se presenta la proposición de que la bisectriz interna del ángulo de un triángulo divide el lado opuesto en dos segmentos proporcionales a los otros dos lados. Contiene 4 Definiciones y 33 Proposiciones (33 ).
El Libro VII es relativo a los Fundamentos de la teoría de los números. Debido a la riqueza de la temática propuesta, a diferencia de los libros anteriores, se permite la conformación de un bloque junto con los Libros VIII y IX en donde se completan algunos temas siempre relativos a las teoría de los números. Entre los tres, comprenden 102 proposiciones que podrían considerarse como la sistematización del legado aritmético de raíces pitagóricas. El Libro VIII y IX, repito, completan esta especie de compendio de aritmética.
El Libro X es el de Clasificación de los inconmensurables, es decir que trata de los números irracionales y consta de 16 definiciones repartidas en 3 grupos y 115 proposiciones.
El Libro XI es el de la Geometría de los sólidos y forma con los siguientes una nueva trilogía que atañe a la geometría del espacio. Hay 75 proposiciones, 63 de las cuales son teoremas y las demás, problemas.
El Libro XII se refiere a Medición de figuras y tiene 18 Proposiciones.
El Libro XIII comprende los Sólidos regulares, que incluyen los 5 sólidos platónicos, a saber: tetraedro, hexaedro, octoedro, dodecaedro e icosaedro. Presenta 18 Proposiciones.
¿Qué aplicación le da la Geología a sus teoremas y postulados?
Si ustedes se han tomado el trabajo de leer en detalle la descripción del libro Elementos, que les puse en la pregunta anterior, podrían contestar solitos a esta nueva interrogación…y estoy tentada de dejar que lo hagan…
Pero no, no se asusten, haremos la revisión juntos.
Lo primero que puede considerarse importante y novedoso, es su concepto de las dimensiones que implica una gran capacidad de abstracción.
Él supone que un punto no tiene tamaño; que una línea es un conjunto de puntos que no tienen ni ancho ni espesor sino solamente longitud; que una superficie no tiene espesor, etcétera. A partir de allí es que se le atribuye al punto, una dimensión nula, a la línea la dimensión igual a uno, a la superficie dimensión dos (ancho y largo) y al cuerpo sólido o poliedro, la dimensión tres.
Esto fue un pilar fundamental del conocimiento espacial al menos hasta la irrupción de la relatividad que incorpora al tiempo.
Por otra parte, ya desde el Libro I se alimenta a la Geología, ya que ésta se vale de la resolución de triángulos para establecer muchos valores de la topografía, como por ejemplo definir altitudes a partir de mediciones de distancias y ángulos. En este aspecto, es vital el teorema de Pitágoras que pasa a las siguientes generaciones, precisamente en esta recopilación, y que recordarán ustedes que es el que enuncia: «En un triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos».
Hoy por cierto, muchas herramientas virtuales permiten resoluciones instántaneas con sólo ingresar los datos pertinentes, pero todos esos modelos se basan en los conocimientos trigonométricos que nacen en la geometría euclideana, y en los conocimientos previos que ella sistematiza.
Los libros XI a XIII, que se centran en los sólidos regulares, abren el camino a la Cristalografía, que facilita el reconocimiento mineral.
Y por supuesto, toda la Teoría de Números es base fundamental para la estadística, el cálculo de superfices, volúmenes y reservas, y la generación de los nuevos modelos matemáticos que permiten por un lado una mejor comprensión de los eventos geológicos, y por el otro la elaboración de predicciones bastante aproximadas a la realidad.
Euclides no se refirió directamente a la Geología, pero todas las ciencias que lidian entre otras cosas con el espacio y su medición, le deben un impulso poderoso.
¿Qué pasa con la Geometría no Euclideana?
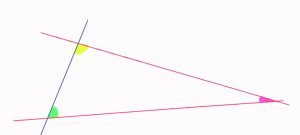
Figura 1
Según este postulado, por un punto exterior a una recta sólo puede trazarse una paralela a ella. Así lo expresó el matemático griego Proclo, y fue la manera que se popularizó con el nombre de axioma de Playfair o postulado de las paralelas.
Otra manera de formular este mismo postulado es la de Euclides:
Si una recta, al cortar a otras dos, forma ángulos internos de un mismo lado que son menores que dos rectos, esas dos rectas prolongadas indefinidamente se cortan del lado en el que están los mencionados ángulos (ver figura 1). La intersección de esas rectas define precisamente el punto externo por el cual sólo una paralela ha de pasar.
Por mucho tiempo se trató de demostrar este postulado como teorema, hasta que en el siglo XIX, algunos trabajos inéditos de Carl Friedrich Gauss (1777-1855) y las investigaciones del matemático ruso Nikolai Lobachevski (1792-1856) dieron el fundamento para la geometría hiperbólica en la que no se cumple el quinto postulado y propiciaron el desarrollo de las geometrías no euclidianas, entre las que vale mencionar la geometría elíptica del matemático alemán Bernhard Riemann (1826-1866), y que luego resultaría más consistente con el modelo de espacio-tiempo relativista.
Para toda geometría que no introduzca el modelo con la cuarta dimensión atribuida al tiempo, la Geometría Euclideana sigue vigente con escasas correcciones.
LOS CINCO POSTULADOS DE EUCLIDES:
1. Se puede trazar una línea recta que pase por dos puntos.
2. Se puede prolongar una línea recta indefinidamente a partir de una recta finita.
3. Se puede trazar una circunferencia con centro y radio dado.
4. Todos los ángulos rectos son iguales.
5. La suma de los ángulos interiores de cualquier triángulo es 180°.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.
P.S.: Las dos imágenes que ilustran el post son de Wikipedia.
El top ten de los momentos más risueños que pasé en el campo.
 Así como hice antes otros listados, que serán el germen de futuros posts donde cada uno de los hechos mencionados tengan su protagonismo, hoy le toca a los momentos graciosos que todos pasamos alguna vez en el campo.
Así como hice antes otros listados, que serán el germen de futuros posts donde cada uno de los hechos mencionados tengan su protagonismo, hoy le toca a los momentos graciosos que todos pasamos alguna vez en el campo.
Por cierto, aclaro que cuando se está en el campo durante muchas horas, con trabajos a veces casi rutinarios, el umbral de la risa está muy bajo, y con muy poco se divierte uno, y almacena lindos recuerdos.
Acá va la lista de los diez más memorables:
- Los chanchitos perdidos.
- La foto y el teodolito.
- La compra del mapa y su traducción.
- La parada en la estación de servicio, después de muestrear loess.
- El día en que observamos las aves. Esta anécdota ya se las conté y pueden ir a recordarla en el correspondiente post.
- El sapito en el río.
- El baño vespertino en Cerro Colorado.
- El Dr del Uranio.
- ¿En qué sentido…
- La escala de la fotografía aérea.
Sólo denme tiempo, y les contaré cada una.
Un abrazo y nos vemos el lunes. Graciela.
P.S.: para ilustrar un post que es un recuento de bloopers, elegí una foto que es en sí misma un blooper, ya que fue tomada desde el teleférico sobre Caracas…pero detrás de un vidrio que estaba completamente esmerilado y además mugriento. Eso es lo que salió….