Locos por la Geología

Archivo de la categoría ‘Geología para principiantes’

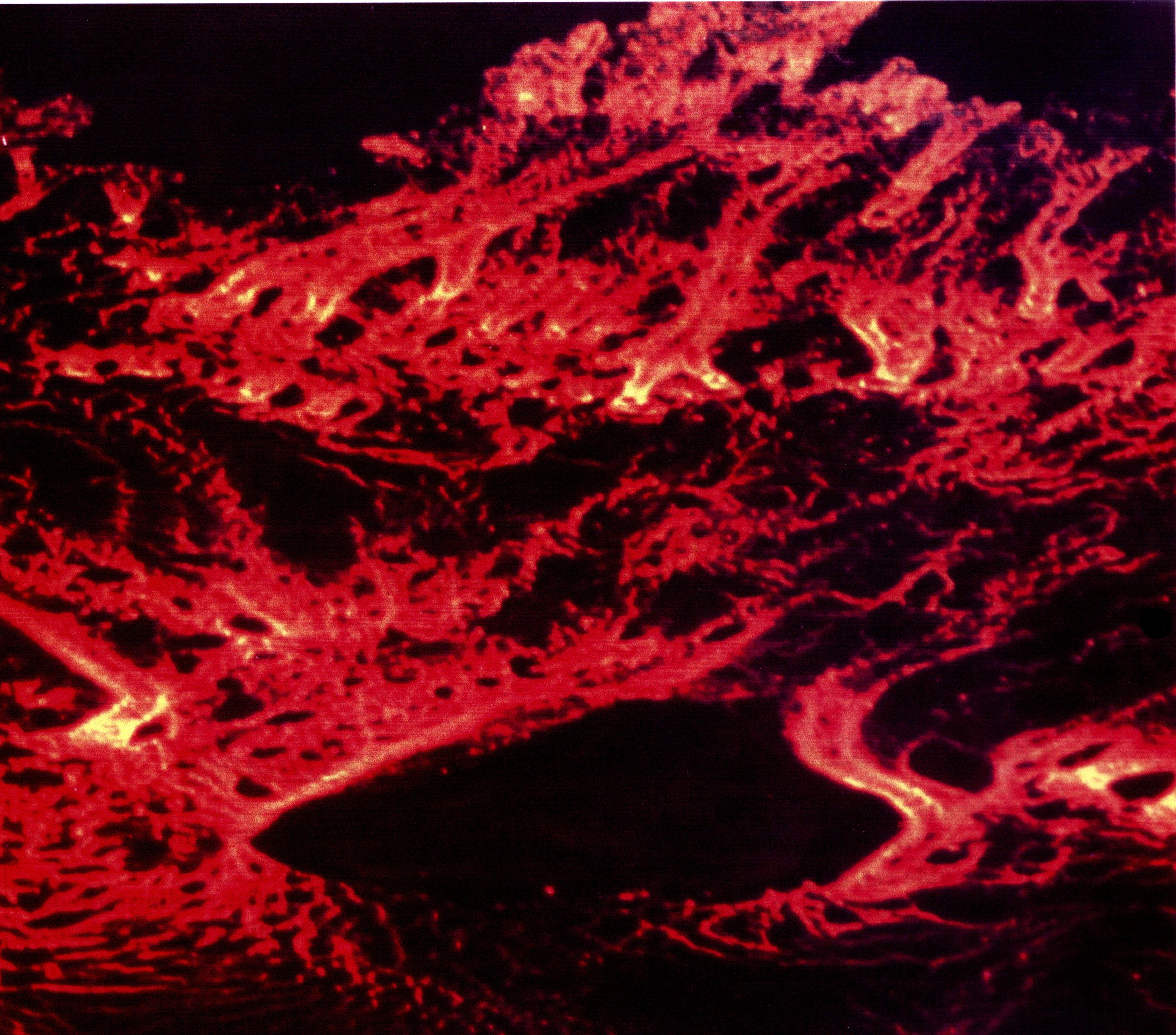Ya les he explicado antes qué es y cómo se origina el magma, y les recomiendo que vean esos posts antes de internarse en éste.

¿Existe un solo tipo de magma?

No, ya lo dije en el post que les mandé a ver hace un momento. Habiendo tantos factores involucrados en la generación de un magma, obviamente los cuerpos magmáticos resultantes serán muy variados.

Es de esa variabilidad de la que hoy hablaremos.

¿Cómo pueden clasificarse los magmas?

Tal como también he dicho muchas veces, existen numerosos criterios para clasificar un universo de objetos, (y hasta de sujetos) y cada cual puede elegir el criterio que prefiere, e inclusive ir cambiándolo en distintas oportunidades para separar esos objetos, de acuerdo con el objetivo que se persigue en cada situación.

¿Cuáles son algunos de esos criterios?

Muchas de las clasificaciones se basan en el tipo de rocas a que los magmas darán origen. Por ejemplo puede hablarse de magmas graníticos o basálticos, etc. Otros, en cambio, apuntan al grupo de minerales que cristalizarán a partir de ellos, y se hablará de máficos o félsicos, cosa que será¡ tema de otros posts. Pero no son ésas las clasificaciones que hoy elijo para este post.

¿Qué criterios preferimos aquí y por qué?

Ninguno de los criterios anteriores me conforma en esta instancia porque apuntan a las rocas resultantes, lo cual implica obviamente la desaparición del magma, puesto que las rocas se forman precisamente a expensas de él.

Por esta razón, esos conceptos no me resultan aplicables a la hora de separar magmas, todavía en su estado fundido.

Por otra parte, nunca pierdo de vista que me estoy dirigiendo a principiantes en el tema, de manera que voy a utilizar una clasificación de comprensión muy sencilla.

Se trata de una división basada en la mayor o menor abundancia de sílice (dióxido de silicio) en la mezcla, lo cual se refleja a su vez en el pH (acidez o basicidad) del magma. Hago notar que esa sílice puede luego formar tanto cuarzo como otros silicatos, cosa que es importante, porque muchas veces para los principiantes eso genera alguna confusión. La abundancia de sílice no es necesariamente abundancia de cuarzo, lo repito una vez más.

¿Cómo se clasifican los magmas según este criterio?

En el marco que yo elijo en esta instancia, los magmas pueden ser:

• Ácidos: son aquéllos que tienen 65 % o más de sílice.
• Mesosilíceos: son los que contienen entre 52 y 64% de sílice disponible.
• Básicos: tienen entre 44 y 51% de dióxido de silicio.
• Ultrabásicos: con menos de 44% de sílice.

¿Por qué es importante conocer el tipo de magma dominante en una cámara dada?

Por muchas razones. Para comenzar, la composición del magma define los minerales que se forman a partir de él, y que a su vez son los que determinan las rocas resultantes.

La composicón también tiene relación directa con los puntos de fusión involucrados, y esto da lugar a distintos rangos de temperatura, tanto para que el magma se origine, como para que se solidifique. Puede generalizarse que los magmas del extremo básico y ultrabásico tienen puntos de fusión más altos, con lo cual son más calientes, lo que los hace más fluidos, y les permite desplazarse a mayor velocidad. El requerimiento de mayor temperatura para la fusión, los hace además, solidificar más velozmente al salir de la cámara, ya que un ligero descenso de temperatura los pone por debajo del punto de fusión requerido, y los coloca en el campo sólido. No obstante lo cual, la cámara en su conjunto se enfría más lentamente porque parte de una temperatura original más alta.

Los ácidos, obviamente serán más fríos y viscosos, y su desplazamiento será lento, con muchas posibilidades de generar taponamientos con severas consecuencias de las que hablaremos en otro momento.

Las modalidades de enfriamiento, serán también factores importantes en la fábrica de las rocas que se originen en cada tipo de magma, de modo que todo eso será conversado en diferentes posts.

¿El magma de una misma cámara puede cambiar con el tiempo?

Sí, y esto es un punto de muchísima importancia. Existen procesos como la diferenciación y la asimilación magmática, que junto a otras causas menores, dan al magma una agitada vida llena de cambios que también nos darán mucha tela para cortar. Pero eso ya es otra historia…

Espero que les haya gustado el post, así nos encontramos el miércoles con información de interés.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente, porque todo está protegido con IBSN 04-10-1952-01.

Figura 1. elipse.

Este post es la continuación del que subí el lunes pasado, que me resultó³ un poco extenso porque, como me pasa siempre, me entusiasmé demasiado escribiendo. 😀 .

Las preguntas que allí respondí son las siguientes:

¿Quién era Kepler y cuándo formuló sus leyes?

¿Cuántas son y a qué se refieren las leyes de Kepler?

¿Qué dice la primera ley de Kepler?

Y hoy retomamos desde allí.

¿Qué es una elipse?

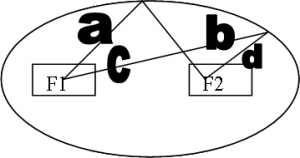
Es el lugar geométrico de todos los puntos para los cuales la suma de las distancias a dos puntos fijos, llamados focos, es constante. (Vean la Figura 1).

Esto se puede decir más fácil a través de una fó³rmula, aunque no lo crean, y es la siguiente:

a+b=c+d

En otras palabras, no importa dónde se paren ustedes a lo largo de la figura de una elipse, siempre la distancia desde ese punto al foco f1, más la distancia desde ese mismo punto al foco f2, será exactamente la misma, vale decir, que permanece «constantemente constante». 😀 .

Respecto a la otra palabreja, la excentricidad, se refiere a la medida de la desviación respecto a la circunferencia en que mejor se inscribe. Cuanto más se aproxima la relación entre ambos perímetros a 1, más parecida al círculo es la elipse correspondiente. Cuando se dice que las órbitas de los planetas son poco excéntricas, se está diciendo que no son excesivamente alargadas, como lo son, por ejemplo, las de los cometas.

¿Qué dice la segunda ley de Kepler?

El radiovector que une el sol con el planeta, recorre áreas iguales en tiempos iguales. Para esto, cada planeta se desplaza con mayor velocidad en la porción de su órbita más cercana al Sol. (Figura 2)

Para entender mejor la figura, les aclaro que en cada caso, el segmento entre los puntos a, b,c, y d, y el sol, está representando distintas posiciones del radiovector a lo largo de la órbita del planeta. O sea, marca el mismo radiovector, que se va desplazando. Y el planeta aparece dibujado dos veces, porque se trata de dos momentos distintos de su recorrido, pero obviamente es único.

En dos momentos diferentes, el área barrida por ese radiovector está representada por los triángulos circulares marcados como E y F. Y si ustedes se fijan, uno es más largo y flaco, y el otro más cortito y ancho, con lo cual (aunque el dibujo no está hecho a escala) E y F pueden considerarse áreas iguales.

Ahora bien, si esas dos áreas iguales (E y F) se barren en tiempos iguales, surge una consecuencia importante, que veremos ahora.

Fíjense no ya en el área sino en el borde solamente, es decir en la propia trayectoria del planeta. Entre a y b hay más distancia que entre c y d.

Pero la velocidad es igual al espacio sobre el tiempo, y si el tiempo no cambia, pero el espacio crece, necesariamente la  velocidad ha de aumentar en a-b, que es casualmente cuando el planeta está más próximo al Sol.

Digámoslo de otra forma, si me mandan a caminar entre la plaza y mi casa, distante diez cuadras, en dos horas, y después me dicen que en el mismo tiempo tengo que ir, en cambio, hasta el límite de la Provincia- a cientos de kilómetros de distancia-, sucederán dos cosas:

1. tendré que correr mucho más rápido y
2. lo mismo no voy a llegar ni a palos.

Pero, concéntrense en la situación 1 que es la que quería demostrar.

¿Qué explicación tiene este fenómeno?

Actualmente, esto puede explicarse en términos de energía. En una órbita elíptica, donde la distancia entre el cuerpo central y el que se mueve a su alrededor no es constante, la energía gravitacional requerida por el sistema disminuye cuando el cuerpo orbitante se acerca al central. En ese momento, la energía gravitacional excedente se transforma en energía cinética, que acelera al cuerpo. Inversamente, al alejarse la masa externa de la central, la energía cinética se transforma en gravitacional, perdiéndose así velocidad.

Esto se repite cíclicamente, y es resultante de la ley de la Gravedad que ya les expliqué en otro post.

Para su tranquilidad, lo puedo explicar más fácil. Si estoy corriendo alrededor de la calesita en movimiento, tomada del borde, es mejor que me agarre con las dos manos y estaré ocupando demasiada energía en no soltarme como para poder correr a mucha velocidad, pero si en cambio estoy asegurada a ella, digamos por un soporte rígido que me asegura que no saldré despedida, me quedará resto para correr mucho más rápido. Por las dudas no hagan la prueba, me alcanza con que entiendan el punto que quiero demostrar.

¿Qué dice la tercera ley de Kepler?

Los cuadrados de los tiempos de las revoluciones son proporcionales a los cubos de las distancias medias de los planetas respecto al Sol.

Esta ley se relaciona conceptualmente con la anterior, más lejos, menos velocidad.

Pero en este caso estoy hablando no ya del mismo planeta a lo largo de su recorrido, sino que estoy relacionando los planetas unos con otros, y viendo la proporcionalidad que existe entre sus posiciones y velocidades.

¿Cuál es la importancia de estas leyes?

Pues ellas permiten predecir y comprender todos los movimientos planetarios. Y por otra parte, señalan el pasaje desde lo que era antes una mezcla de ciencia, mitos, creencias, astrología mágica y especulaciones, a una astromía fundamentada en hechos explicables de modo racional.

Un abrazo y hasta el miércoles. Graciela

Este post lo he construido sobre la base de un apunte de mi propia autoría que se identifica como sigue:

Argüello, Graciela L. 2006.» La Tierra como planeta integrante del Sistema Solar» Cuadernillo didáctico Nº II, Capítulo 1. Para circulación interna en la U.N.R.C. 17 páginas.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque está registrado con IBSN N° 04-10-1952-01.

Si ustedes han venido leyendo los numerosos posts etiquetados con la palabrita Cosmos, tendrán ya un panorama útil para ubicar a la Tierra en su contexto, como lo que es, una partícula apenas, en un todo que la contiene y que la condiciona.

Hasta este momento ya hemos mencionado y explicado un poco sobre los planetas que forman, con el nuestro, la corte que acompaña al Rey Sol en su viaje por el Universo.

Es hora entonces de detenernos para analizar, siquiera brevemente las leyes que explican algunas relaciones y regularidades del Sistema Solar.

Ya les he explicado la ley que podríamos considerar como la más universal y fundamental, válida para el Sistema y el Cosmos todo, que es obviamente la de la Gravedad.

Ahora vamos a ver un grupete de leyes más de acá nomás, del «barrio planetario», o sea las Leyes de Kepler.

Empecemos pues.

¿Quién era Kepler y cuándo formuló sus leyes?

Johannes Kepler (1571 – 1630), fue un personaje clave en la revolución científica, a través de su tarea como astrónomo y matemático. Nació en Alemania y luego de ser por un año colaborador de Tycho Brahe- matemático imperial de Rodolfo II- le sucedió en tal cargo cuando se produjo su deceso. A favor de las observaciones que le dejara Tycho Brahe, y las suyas propias, en 1601 elaboró las leyes que hoy nos ocupan.

La vida de Kepler es apasionante, pero hay algunas notas de color que merecen distraernos por un momento, antes de volver a las Leyes que le valieron un lugar en la historia de la Ciencia.

La madre de Kepler ejercía como curandera y herborista, y era seguramente una apasionada de los fenómenos naturales, pues fue ella quien lo acompañó a un lugar descampado y alto para observar el paso del cometa Halley en 1577. Esos intereses poco comunes le valieron una acusación de brujería, y fue precisamente Kepler quien la salvó de la tortura y la hoguera, tras dedicar largos años a redactar y presentar alegatos en su favor.

Kepler se casó dos veces, y tuvo un total de doce hijos, pero sólo la mitad de ellos llegaron a la edad adulta. Él mismo, que siempre había sido enfermizo, murió en Baviera a los 59 años.

En 1632, (dos años después de su muerte), en medio de la Guerra de los Treinta Añs, el ejército sueco destruyó su tumba y sus trabajos desaparecieron hasta 1773, cuando fueron afortunadamente recuperados por Catalina II de Rusia.

Por la enorme importancia de su obra, una cadena montañosa del satélite marciano Fobos fue bautizada como  «Kepler Dorsum» en su homenaje.

Hay por lo menos otros dos datos que merecen ser destacados en la vida de este sabio.

Por un lado, si bien varios astrónomos pudieron observar en 1604 la ocurrencia de una supernova en la Vía Láctea, fue Kepler quien llevó a cabo su estudio en detalle. Por esa razón, esa supernova, que fue la única observada y descrita en tiempos históricos dentro de nuestra propia galaxia, a sólo 13.000 años luz de distancia, fue denominada Estrella de Kepler.

Y el último dato de interés es que entre sus numerosas obras, figura «Somnium sive Astronomia lunaris», (El sueño o Astronomía de la Luna) que hoy se considera como el primer intento de novela de ciencia ficción del que se tiene conocimiento.

¿Cuántas son y a qué se refieren las leyes de Kepler?

Las leyes de Kepler son tres, y explican las relaciones dinámicas entre los movimientos de los planetas y el Sol. Es decir que expresan el modo en que se producen los movimientos de traslación en el Sistema Solar.

¿Qué dice la primera ley de Kepler?

Los planetas describen órbitas elípticas poco excéntricas, en uno de cuyos focos está el Sol.

Esto destierra la idea de círculos perfectos con que hasta muy poco tiempo antes se pretendía explicar los movimientos de los planetas.

Pero requiere un par de aclaraciones que veremos en la parte 2 de este post, que podrán leer el próximo lunes, a la misma hora y por el mismo canal 😀 .

Para ese post les prometo responder a las preguntas que ven más abajo. ¿Nos vemos entonces?

¿Qué es una elipse?

¿Qué dice la segunda ley de Kepler?

¿Qué dice la tercera ley de Kepler?

¿Cuál es la importancia de estas leyes?

Un abrazo y hasta el miércoles. Graciela

Este post lo he construido sobre la base de un apunte de mi propia autoría que se identifica como sigue:

Argüello, Graciela L. 2006. «La Tierra como planeta integrante del Sistema Solar» Cuadernillo didáctico Nº II, Capítulo 1. Para circulación interna en la U.N.R.C. 17 páginas.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque sus contenidos están registrados con IBSN 04-10-1952-01.

P.S.: La imagen que ilustra el post procede de este sitio.

Estoy segura de que cualquiera de ustedes, haya o no estudiado Geología alguna vez, ha escuchado este término muy a menudo.

Y también estoy segura de que todos saben que estamos por referirnos a las aguas subterráneas.

Pero como pasa casi siempre en este tema, hay mucho más implícito en el término de lo que se suele evocar en primera instancia. Y de eso vamos a hablar.

Comienzo por recordarles que ya hemos visto un ciclo del agua bastante más completo de lo que se suele leer en el colegio; y más adelante nos referimos a las rocas que por ser porosas y permeables permiten la filtración de aguas que se acumulan a diferentes profundidades, en lo que dimos en llamar acuíferos.

Ahora seamos un poco más exquisitos y desmenucemos los conceptos relacionados con esa palabreja.

¿Cuál es la etimología de acuífero?

El término procede de la unión de dos vocablos latinos: aqua= agua y feros= llevar, trasladar, transportar o portar. Es decir que se usa para referirse a algún elemento, en este caso rocas, que pueden trasladar el agua.

Recuerden entonces que el agua subterránea sólo en muy escasas situaciones se mueve subsuperficialmente como un río.

Por el contrario, el caso común es que esté saturando los espacios porosos de los materiales litológicos en que se encuentra. Al moverse, en esas circunstancias, el agua lo hace gota a gota, pasando de un poro a otro, siempre que ellos estén conectados entre sí es decir si hay permeabilidad.

¿La palabra acuífero tiene más de un significado?

Sí, como pasa muchas veces en Geología, para la palabra acuífero hay un sentido estricto y otro amplio o extendido. Ahora distinguiremos entre ambos.

¿Cuál es su sentido estricto?

El empleo más específico de la palabra acuífero, es para designar a aquel tipo de material geológico que permite el paso del agua.

Es decir que se usa para caracterizar un tipo de roca, y por ello forma parte de una clasificación de las mismas, según cómo se comportan ante el avance del agua.

¿Cómo se clasifican los materiales de la corteza terrestre según su capacidad de conducción del agua?

Según la combinación de su porosidad y permeabilidad, los materiales podrán o no ser atravesados por el agua, lo cual permite dividirlos en:

• Acuíferos: son sedimentos, capaces de conducir el agua, pues poseen los requisitos de porosidad y permeabilidad. En otras palabras, el agua puede atravesarlos sin oposición.
• Acuícludos: son materiales porosos, pero no permeables, que por esa razón retienen el agua, ocluyéndola en espacios de los que no puede salir, ni, por ende extraerse. Pueden ser no solamente sedimentos sino también rocas, como por ejemplo los basaltos con espacios huecos debidos al escape de gases. El problema es que los espacios están aislados entre sí, y por eso el agua se estanca en ellos, pero no circula.
• Acuífugos: son cuerpos que no permiten la penetración del agua por carecer de porosidad y permeabilidad, y que favorecen en cambio el escurrimiento.
• Acuitardos: son materiales con porosidad y permeabilidad, que en principio permiten el pasaje del agua, pero que por rasgos secundarios, como relleno de parte de los poros con material más fino, etc, disminuyen la velocidad del flujo.

¿Cuál es el sentido extendido de la palabra acuífero?

Éste es precisamente el que más escuchamos en la vida corriente, cuando los informativos por ejemplo, nos preocupan advirtiendo que se están contaminando los acuíferos, o que han subido algunos o bajado otros.

En este caso, no estamos hablando de un tipo particular de material geológico, sino de un reservorio subterráneo de agua, en el que un material de tipo acuífero es parte fundamental, pero no única ni suficiente.

En efecto, un acuífero (stricto sensu) puede ser atravesado por el agua, pero eso no presta ninguna utilidad a los habitantes de una zona, si no se da otro requisito concurrente.

Digamos que sería como un pueblo sin parada de colectivo, uno podría verlo pasar pero al no detenerse, no serviría de nada, ya que nadie subiría ni bajaría en el lugar. El colectivo tiene que parar para que sea accesible.

Y lo mismo pasa con el agua, para que se genere un reservorio, el acuífero (s.s.) debe estar en contacto con otros materiales que no permiten la circulación.

En ese caso, se denomina acuífero (sentido amplio) al sistema constituido por el material acuífero propiamente dicho, y el acuícludo que impide que el agua siga circulando. Es a partir de ese sistema que puede explotarse el agua subterránea, que de lo contrario pasaría de largo dejándonos muertos de sed en el camino.

Algo así como si nos sirvieran agua en un colador.

¿Existen distintos tipos de acuíferos?

Sí claro, pero no sean tan inocentes como para pensar que se pueden explicar en dos palabras y aquí. Esta pregunta es un anzuelo que les tiro para que se enganchen con algún post que subiré un lunes cualquiera, así que manténgase alertas, no se les vaya a pasar el agua…

Un abrazo y hasta el miércoles. Graciela.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuenteporque esta página está registrada con IBSN 04-10-1952-01..

P.S.: La imagen que ilustra el post vino en una cadena de mails, no conozco al autor.

Este post es la continuación del del lunes pasado, razón por la cual les recomiendo que vean primero ese texto si todavía no lo han hecho, para poder comprender éste en su totalidad.

Las preguntas que nos habían quedado por contestar hoy son las siguientes:

¿Cómo se calculó inicialmente la Constante Universal de la Gravedad, y cuánto vale?

Ya les aclaré la semana pasada que hoy sólo iba a hacer mención del método utilizado y de su autor, pero todo el experimento amerita un post completo que subirá dentro de poco al blog. Vale la pena y se puede explicar de manera sencilla, si nos tomamos el tiempo necesario.

Así pues, hoy sólo les digo que el primer experimento exitoso sobre cuya base se pudo establecer el valor numérico de la constante gravitacional G, fue realizado más de un siglo después de la formulación de la Ley por Isaac Newton.

La primera determinación se hizo repitiendo un experimento que realizara Lord Cavendish, a través de un ingenio que hoy se recuerda como la Balanza de torsión o de Cavendish.

Cavendish, en realidad lo que hizo en 1798, en su propia casa, conocida como Clapham Common, fue definir la densidad de la Tierra, sin darse cuenta de que el mismo experimento serviría unos 75 años más tarde para establecer el valor de G .

Insisto en que el experimento mismo lo explicaré más adelante, pero el valor que se obtuvo para la constante universal de la gravedad fue de

6,67 x 10 ^-11 N m ²Kg ^-1

La unidad de medida incluye: Newton como medida de fuerza; metros al cuadrado porque el valor de la distancia en la fórmula original es cuadrático; y Kg a la menos uno, indicando que forma parte de un denominador. El exponente menos 11 indica que el valor 6,67 debe dividirse por la unidad seguida de once ceros.

¿Por qué se habla de un valor constante por un lado, y por el otro se dice que la gravedad en otros planetas es mucho mayor o mucho menor que en la Tierra?

Por un lado porque dentro de la Fuerza gravitacional interviene un solo factor (G) que es constante, mientras que los demás son variables, y por otra parte porque si bien ese 6,67 etc., etc., que aparece como valor para G es único en el universo, cuando se compara la gravedad en la Tierra y en la Luna, de lo que se está hablando es de otro parámetro, que es la «aceleración de la gravedad», que paso a explicarles ahora.

Para entender mejor el concepto de aceleración de la gravedad, debemos recordar primero que una fuerza cualquiera se define según la fórmula F= m x a, en donde:

F= es la fuerza

m= es la masa afectada por dicha fuerza.

a= es la aceleración que la fuerza imprime sobre la masa en cuestión.

Como toda expresión matemática, es absolutamente lógica y sencilla de explicar en términos corrientes. Piénsenlo en estos términos: la fuerza es tan grande como lo es la masa que empuja, y cuán «rápidamente» consigue moverla.

En otras palabras, si uno empuja un chancho, hace más fuerza que si empuja a un pollito, y si a ese chancho lo hace desplazarse como una tortuga, obviamente le aplicó menos fuerza que si lo mandó como un cohete a aterrizar en el medio del patio. Consecuentemente, la fuerza es el producto de ambas cosas: la masa que se mueve y la aceleración que se le imprime.

Ahora vayamos a revisar nuestra fórmula de la gravedad universal, la que aprendimos en el post del lunes pasado (¡ya les avisé que tenían que repasarlo!) Recuerden que el 2 es un exponente, vale decir que se lee como r al cuadrado.

F= G m.m’
         r²

Ahora, por el solo hecho de que sirve a nuestros fines, reemplazamos en la fórmula la fuerza por su equivalente: masa por aceleración, y ¿qué pasa?

m x a= G m.m’
                r²

Si despejamos (como se decía antes, cuando nosotros estudiábamos) el valor de la aceleración a, o lo que es lo mismo, dividimos por m ambos términos, con lo cual la igualdad permanece, nos queda lo siguiente:

 a= G m.m’
      m x r²

Es obvio que dividir m por m es igual a 1, que como factor en un producto no tiene ninguna importancia, es decir que puede quitarse de la ecuación sin problemas, con lo cual nos estamos independizando del valor de la masa exploradora.

En otras palabras, la aceleración de la gravedad tiene la ventaja de ser solamente dependiente de la masa omnipresente en cada lugar: en nuestro caso de la de la Tierra, en la Luna de la de ésta y en Marte de la que ese planeta tiene.

Ésa es pues la medida gravitacional que varía de un sitio a otro en el Universo. La fórmula de la aceleración queda pues así:

a= G m’
        r²

Es práctica corriente llamar a la aceleración de la gravedad directamente g (minúscula, para distinguirla de G. la constante universal)

En otras palabras, en cada lugar la aceleración gravitacional sobre cualquier cuerpo es solamente el resultado de la constante por la masa del lugar, y es inversamente proporcional al cuadrado de la distancia entre ambos (el cuerpo y la concentración de masa del sitio).

¿Cuánto vale la aceleración de la gravedad promedio en la Tierra?

La unidad de aceleración de la gravedad es el Gal, definido en honor a Galileo, y corresponde a cm x s ^-2  ,que como ya saben se lee centímetros sobre segundos al cuadrado.

El valor numérico promedio es 980, vale decir 980 gals o 980 centímetros sobre segundos al cuadrado. Este valor en la Luna es unas diez veces menor, por ejemplo, y por esa razón los astronautas «flotan» en ella. O sea que si ustedes están buscando infructuosamente perder peso, con sólo ir a la Luna, pesarín diez veces menos, aunque siguieran igual de gorditos. 😀 . (Esto es un dato realmente al cuete, pero le da color a la cosa).

¿La aceleración de la gravedad es absolutamente invariable en el mismo cuerpo planetario?

No, ni siquiera en el mismo cuerpo planetario es totalmente constante, y eso es así porque hay numerosos factores que inciden en la sencillísima fórmula que hemos analizado. Por ejemplo, si estamos en una montaña, nos hemos alejado de la concentración de la masa que teóricamente está en el centro del planeta. También es distinta la masa involucrada por encima de un yacimiento de hierro, de la que hay sobre el mar o sobre una planicie de loess, pues las densidades son muy distintas también.

De cualquier modo, la variación es tan pequeña de un sitio a otro, que la unidad Gal resulta excesiva y se ha creado por ello el miligal, que es obviamente mil veces más pequeña. A veces las variaciones de un sitio a otro son del orden de un miligal, o hasta de una fracción de miligal.

De todo esto podría armar un post en el futuro, si les interesa.

¿Qué utilidad tiene esa característica de cierta variabilidad?

Mucha, muchísima, ya que esto permite realizar prospecciones gravimétricas, en las cuales las variaciones medidas pueden denunciar cambios en los terrenos por sobre los cuales se toman las correspondientes mediciones. Es una técnica geofísica muy aplicada en minería y sobre todo en petróleo.

Además, permite describir la geología profunda, a los solos fines de incrementar el conocimiento, es decir forma parte de metodologías de investigación tanto básica como aplicada. Pero eso da muuuucho que hablar y lo haremos en otra oportunidad.

Un abrazo y hasta el miércoles. Graciela.

Este post lo he construido sobre la base de un apunte de mi propia autoría que se identifica como sigue:

Argüello, Graciela L. 2006. » La Tierra como planeta integrante del Sistema Solar» Cuadernillo didáctico Nº II, Capítulo 1. Para circulación interna en la U.N.R.C. Versión totalmente actualizada.17 páginas.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

La imagen que ilustra el post la he tomado de la página de la Cátedra de Geofísica de la Universidad de La Plata, y representa los gravímetros utilizados en prospección.