Entradas con la etiqueta ‘Agua’
Un proyecto amigable con el ambiente, realizado en la India.
 Hoy, como un mensaje esperanzador, he rescatado un ejemplo de recuperación ambiental que ya tiene más de 20 años de implementación. y que vale la pena conocer.
Hoy, como un mensaje esperanzador, he rescatado un ejemplo de recuperación ambiental que ya tiene más de 20 años de implementación. y que vale la pena conocer.
¿Cuál es en general la situación ambiental en India?
La polución del agua de los cursos superficiales en la India es una realidad que se agrava con el incremento poblacional que caracteriza a ese país. El sistema cloacal tradicional no es viable en las condiciones de pobreza de las comunidades rurales, que no pueden afrontar el alto costo de su instalación donde la infraestructura preexistente es prácticamente nula.
¿Dónde se implementó el proyecto que hoy nos ocupa?
Este proyecto data de la última década del siglo pasado, y se instaló en la ciudad de Pune, en el estado de Maharashtra, y en las cercanías de Bombay; prácticamente en el límite entre India del Norte e India del Sur.
¿Cuál era el problema específico en el lugar seleccionado?
La zona sobrellevaba los problemas típicos del cinturón de los monzones de verano de India central y septentrional. Es decir que durante todo el año se acumula basura de cualquier origen, a la espera de que el propio monzón se ocupe de llevarla. Los excedentes de los tanques sépticos drenan en las llamadas «nalas», que no son otra cosa que canales de drenaje urbanos a cielo abierto, que cuando pasa el monzón concentran los desechos, generando verdaderas cloacas expuestas.
Esas nalas, tarde o temprano se vierten en los arroyos y ríos que hasta son utilizados para riego entre otras cosas. El riesgo para la salud es altísimo.
El sitio específico escogido para el proyecto fue un espacio yermo y perteneciente al estado, que ocupa alrededor de 6 hectáreas distribuidas en una estrecha franja de unos 900 metros de longitud y de entre 60 y 70 de ancho. Esa franja bordea una corriente iniciada en una planta de tratamiento de aguas, que se había ya convertido en una cloaca, al atravesar diversos barrios precarios.
Respecto al uso de la tierra, había estado sometida a sobrepastoreo de cabras y ocupada por cerdos y otros animales asilvestrados, con lo que el suelo había llegado hasta tal extremo de erosión que era inutilizable, y se observaban rocas aflorantes. Respecto a la vegetación sólo se contabilizaban dos árboles de neem (Azadirachtra indica), y una palmera Palmyra (Borassus flabellifer), sobreviviendo apenas.
De resultas del proyecto, esa zona es hoy un bellísimo parque, pero vayamos de a poco.
¿Cuál fue la propuesta para el proyecto?
La idea central fue crear un parque cuyas aguas serían provistas a partir de un sistema de limpieza, tratamiento y purificación de las aguas que las nalas conducen hasta el lugar. Todo el sistema implicaría pocas construcciones y modificación mínima del relieve prexistente, aunque sus efectos significarían un cambio sustancial en el estado del espacio involucrado. Sería por supuesto un cambio positivo que terminaría creando un nuevo ecosistema mucho más sano y totalmente sostenible.
¿Cuáles fueron los requisitos para la implementación?
Dos se consideraron requisitos previos: excluir la cría de cabras en la zona, y reubicar los animales silvestres por un lado; y reducir la contaminación activa del agua de la corriente principal. Sólo después podría abrirse el parque para usos recreativos.
Para poder cumplir con el segundo requisito, fueron imprescindibles numerosos estudios, algunos muy relacionados con nuestra ciencia geológica (por eso este post está aquí, ;D ), especialmente porque se intentaba respetar al máximo la vocación propia del espacio, sólo minimizando los efectos indeseables de las intervenciones previas.
El relevamiento se dirigió a reconocer los siguientes rasgos del – por entonces- futuro parque, y de la corriente que lo acompaña y su área de alimentación.
- Sitio de inicio de la corriente.
- Recorrido del curso y puntos en los que se drenaban efluentes en él.
- Carga polutante.
- Patrones de uso el agua y temas sociales relacionados.
- Calidad del agua y el suelo en el punto de partida.
- Mediciones de flujo a lo largo de todo el año.
- Medidas de evaporación.
- Problemas especiales relacionados con el régimen monzónico.
¿Cómo se implementó el sistema?
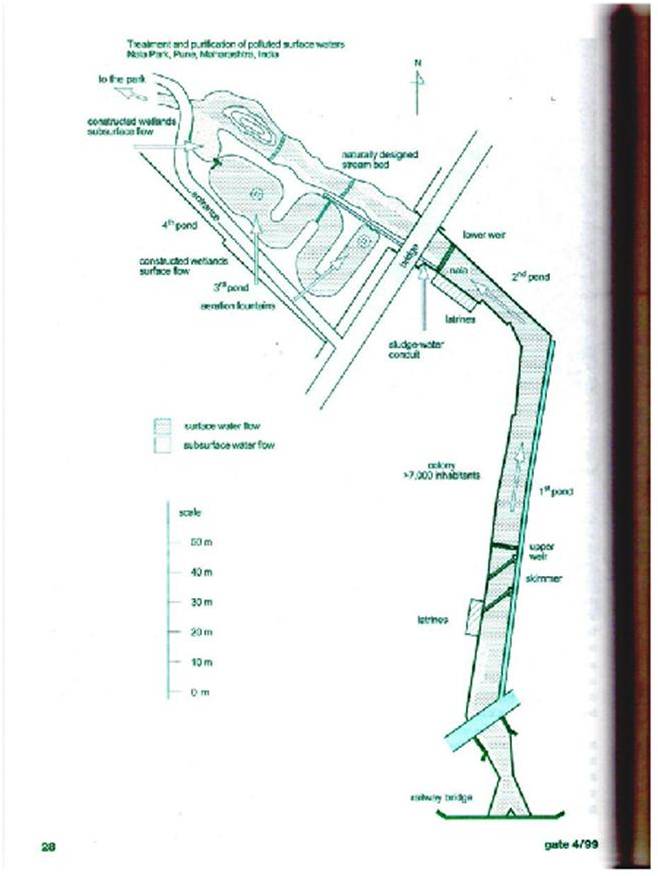
El sistema está esquematizado en la imagen que acompaña el post.
Se limpió la zona urbanizada precariamente (una villa de 7.000 habitantes a lo largo de un tramo de 200 m bordeando la corriente de alimentación del parque), y se instalaron dos piletas de decantación, con compuertas que se abren para permitir el paso de los excesos hídricos en las épocas de monzones. Hay una caída de 30 cm entre ambos diques, y son permanentemente monitoreados para corregir cualquier desvÃo en la carga admisible. Además se sembraron allí peces denominados Gambusia que se alimentan de los mosquitos que podrían proliferar en las piletas. También se controla periódicamente la salud de la población de gambusias.
Aguas arriba, los drenajes de la villa se aislaron mediante paredes de contención para que los excedentes monzónicos no afectaran el agua limpia de la corriente principal.
Más abajo de la segunda pileta, y desde el fondo de la corriente se extrae un lodo que continúa su decantación en las piletas N° 3 y 4, mientras sigue fluyendo la parte superficial ya bastante más limpia.
El lodo es desviado hacia los decantadores 3 y 4, con un 80% menos de carga suspendida, respecto al inicio de la instalación.
La pileta 3 está 30 cm más abajo que la 2; y la 4, 20 cm más abajo aún que la 3. Estas dos últimas piletas tienen forma de serpentina para aumentar la longitud de su flujo, y optimizar el uso del terreno disponible.
La salida del decantador N° 4 se conecta de modo subsuperficial, con la corriente original, de modo de devolverle las aguas previamente desviadas de ella, pero ya limpias y claras a la vista.
Todo el sistema funciona tratando continuamente 2.700 litros de agua por minuto; y está diseñado de modo que su flujo máximo durante el monzón pueda alcanzar hasta 200.000 l/minuto, sin dañar el diseño, pues se han dejado espacios que funcionan como llanuras de inundación en esos momentos.
El principal problema a sortear puede ser en determinados sistemas administrativos, la falta de regulaciones compatibles con estas iniciativas, que escapan a las grandes estructuras vigentes.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.
P.S.: La imagen que ilustra el post es de la revista Gate, de donde tomé y traduje la historia de este ejemplo.
El día que se detuvieron las cataratas del Niágara
 Hoy la elección del tema para mi post pasa por la efeméride. Efectivamente, el 29 de marzo de 1848, se recuerda un hecho curioso del que no se cuenta con registros históricos anteriores, y se trata del congelamiento completo de las cataratas del Niágara, fenómeno que duró treinta horas.
Hoy la elección del tema para mi post pasa por la efeméride. Efectivamente, el 29 de marzo de 1848, se recuerda un hecho curioso del que no se cuenta con registros históricos anteriores, y se trata del congelamiento completo de las cataratas del Niágara, fenómeno que duró treinta horas.
Vamos a recordar ese hecho, y usarlo de excusa para señalar algunas cosas más.
¿Dónde quedan y qué características tienen las cataratas del Niágara?
Las cataratas del Niágara – como casi siempre ocurre con las cataratas más imponentes del mundo- no están constituidas por una única caída, sino, en este caso, por al menos tres saltos mayores que detallaremos en seguida; y que se localizan sobre el río homónimo, en la región nororiental de América del Norte, entre Estados Unidos y Canadá. Se encuentran a unos 236 msnm y salvan un desnivel de aproximadamente 64 metros.
Los saltos que mencionaba arriba son:
- La Catarata Canadiense o Horseshoe Fall, en la Provincia de Ontario.
- La Catarata Estadounidense, en el estado de Nueva York.
- La Catarata Velo de Novia, de mucho menor tamaño.
Aunque no tienen una gran altura, sí son las más caudalosas de América del Norte, ya que reúnen toda el agua de los Grandes Lagos. Son valiosas como sitio turístico y como fuente de energía.
¿Qué significa el término Niágara?
Toda la región estaba, a la llegada de los europeos, poblada por una tribu iroquesa, cuyo nombre era ongiara, pero a la que los conquistadores franceses llamaban «los mediadores», pues fueron con ellos muy amigables y facilitadores de su relación con otras tribus.
Según las leyendas de los ongiara, en la cueva que se encontraba tras la Horseshoe Fall, vivía HE-NO, el Dios del trueno, y en el idioma originario, la palabra Niágara significa «trueno de agua». Según esa misma leyenda, el jefe de la tribu concedió la mano de su hija Lelawala a un soldado invasor; pero ella prefirió desobedecerle e irse del poblado, para entregar su alma al Dios del trueno, con quien permanece desde entonces en la catarata.
¿Cuál es el origen geológico de los saltos de agua?
Como el propósito de hoy es simplemente recordar una efeméride, habrá otro post más completo al respecto en el futuro, pero hoy baste con decir que la catarata se originó hace alreddor de 10.000 años, de resultas del avance glaciario que cambió la topografía y el drenaje por completo, dejando como resultado los grandes lagos, cursos y saltos de agua que generaron los grandiosos paisajes que incluyen a las Cataratas que nos ocupan.
¿Además del que hoy se conmemora, hubo otros episodios en que se congelaron las cataratas del Niágara?
Si bien los fenómenos geológicos dejan sus propios registros, en la historia recopilada por el hombre sólo se reconocen tres episodios en que las Cataratas se congelaron de manera completa. Esos episodios son:
- El 29 de marzo de 1848, tras una ola de frío en la que se alcanzaron valores mínimos de -35º C quedaron completamente congeladas. Para que eso ocurriera, fue necesario que primero un gran bloque de hielo la bloqueara permitiendo tan completo congelamiento.
- La segunda ocasión documentada en la historia, fue en 1902 y hay registros de ella en la Biblioteca Pública de las Cataratas del Niágara.
- El último congelamiento completo es del año 1936.
Hay también una imagen bastante famosa y conocida como «Cave of the winds in Winter Niagara Falls», que apareció en una postal de 1911, pero de la que no se sabe si fue de alguno de los dos episodios anteriores, o si también existió un fenómeno similar en ese año.
Existen otros episodios en que los saltos se congelaron, pero sólo parcialmente, como son los casos de 2007, de enero de 2014 y por fin del 23 de enero de 2019, en que tras el paso de la tormenta Harper, la temperatura descendió hasta -20°C.
¿Por qué se dice que no pueden volver a ocurrir esos congelamientos completos?
Como puede observarse, después de 1936 no volvieron a congelarse por completo, lo que en buena medida podría deberse a algún ligero cambio del microclima, inducido por la creación de la planta generadora de la Autoridad de Energía de Nueva York. Aunque esta aseveración no pasa de ser especulativa.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.
P.S.: La imagen que ilustra el post es de este sitio.
La ley de Stokes
 Como un avance más, aplicable tanto a la dinámica fluvial, como a la eólica, y a cálculos de laboratorio, hoy veremos la ley de Stokes y su derivación hacia un caso particular: el de las partículas pequeñas que sedimentan en un fluido. Pero vayamos por partes.
Como un avance más, aplicable tanto a la dinámica fluvial, como a la eólica, y a cálculos de laboratorio, hoy veremos la ley de Stokes y su derivación hacia un caso particular: el de las partículas pequeñas que sedimentan en un fluido. Pero vayamos por partes.
¿A quién debe su nombre la ley de Stokes?
A Sir George Gabriel Stokes, primer Baronet del Reino Unido, un matemático y físico irlandés que realizó contribuciones importantes a la dinámica de fluidos, y a quien se considera como uno de los tres más importantes estudiosos de las ciencias naturales de su época, junto a James Clerk Maxwell y Lord Kelvin.
Fueron ellos tres los que inauguraron la fama de la escuela físico matemática de Cambridge a mediados del siglo XIX.
¿Qué conocemos de Sir Stokes, su vida y su trabajo?
Nació en Skreen, condado de Sligo, Irlanda, el 13 de agosto de 1819, y falleció en Cambridge, Inglaterra, el 1º de febrero de 1903. Sus primeros estudios fueron en Skreen, Dublín y Bristol, pero se graduó en 1841 en Pembroke College, de la Universidad de Cambridge, habiendo obtenido tan altos honores como el título de Senior Wrangler y el Premio Smith.
En seguida fue contratado como profesor, pero en 1857 renunció a su cátedra por haberse casado, lo cual no estaba permitido en los estatutos de su Facultad. Debió esperar doce años hasta la modificación de esos estatutos para retomar la docencia que ejerció en esa Universidad hasta su muerte.
Entre 1885 y 1890 fue presidente de la Royal Society, y a lo largo de su carrera produjo más de un centenar de publicaciones.
Merece destacarse el hecho de que siempre reunía el análisis teórico matemático y la comprobación experimental, lo que dio una gran solidez a sus múltiples contribuciones a la ciencia.
Algunos de los temas que abordó fueron: el movimiento uniforme de fluidos incompresibles, la fricción de fluidos en movimiento, el equilibrio y movimiento de sólidos elásticos y numerosos tópicos de la teoría del sonido. Muchos de sus trabajos impulsaron el conocimiento de la hidrodinámica y fenómenos asociados a ella.
Entre los numerosos honores que se le dispensaron, cabe mencionar que la unidad de medida de la viscosidad cinemática en el Sistema Cegesimal lleva su nombre; como también lo lleva la ley que hoy nos ocupa, un teorema de geometría diferencial, las ecuaciones de Navier-Stokes, de dinámica de fluidos, y los parámetros usados para cuantificar la polarización de las ondas electromagnéticas. Todo eso solamente en el campo de la Ciencia Física, pero también en Astronomía, llevan su nombre un cráter lunar y uno marciano, y el asteroide 30566.
Como si eso no bastara para engrandecer su figura, recibio otras distinciones, como la Medalla Rumford de la Royal Society, la Medalla Copley y el título de Baronet, para citar unos pocos ejemplos. En 1891 publicó sus conferencias Gifford en un volumen titulado Teología Natural.
¿Cuál es la formulación original de la ley de Stokes?
En su formulación original, la ley de Stokes se refiere a una fuerza de fricción, aunque luego veremos que también se conoce con ese nombre a una derivación posterior con la que se miden velocidades de caída de partículas en el seno de un fluido.
Pero no nos apresuremos, inicialmente la ley de Stokes cuantifica la fricción que experimentan objetos esfáricos pequeños que se mueven a baja velocidad dentro de un fluido viscoso en régimen laminar.
La expresión matemática es:
Fr= 6πµvr
donde r es el radio de la esfera, v su velocidad y µ es la viscosidad del fluido. Aclaremos que la viscosidad de un fluido es la medida de su resistencia a las deformaciones graduales debidas a las tensiones cortantes o de tracción. Obviamente 6 pi es constante.
¿Cómo se aplica a la sedimentación de partículas muy finas en un fluido?
Una consecuencia de esa formulación fue obtener la velocidad de caída vertical- sólo debida a su propio peso- de una partícula muy fina en el interior de un fluido. Ese fluido puede ser en la naturaleza, un curso de agua, o el propio viento. Dicha velocidad se expresa en la siguiente formulación matemática:

donde:
V es la velocidad de caída de las partículas;
g es la aceleración de la gravedad;
dp es la densidad de la partícula;
df es la densidad del fluido;
µ es la viscosidad del fluido; y
r es el radio equivalente de la partícula.
Aclaremos que esa velocidad se mide para ciertos supuestos:
- La partícula debe ser esférica. Pero como en la naturaleza la esfera perfecta difícilmente existe, se habla de un radio equivalente, que es aquél que corresponde a la esfera teórica o ideal, en la que mejor se inscribe la partícula real de que se trate.
- La temperatura del fluido debe ser constante, de modo que se mantenga también invariable su viscosidad, ya que de ella depende.
- No debe haber otras fuerzas intervinientes que pueden cambiar el flujo de laminar a turbulento.
¿Qué aplicaciones prácticas tiene esta ley?
Muchas. Para empezar explica claramente por qué partículas muy finas, cuya velocidad de caída es muy baja pueden permanecer en suspensión por largos intervalos, ya sea en la atmósfera, donde los vientos pueden llevarlas a cientos o aun miles de kilómetros de distancia de su fuente de origen; o en los cursos de agua.
Estos datos son importantes a la hora de calcular las plumas de contaminación de las que hablaremos en algún otro post.
Pero además, el cálculo de la velocidad de caída es la base de las metodologías por sedimentación y por densimetrÃa que se usan para calcular la granulometría de la fracción fina de materiales sedimentarios y suelos. Esto se los he explicado en un apunte que puede ver en este post.
También contribuye a entender la gradación de los materiales en columnas sedimentarias, y a reconstruir sistemas de paleocorrientes e interpretar paisajes y relieves, pero eso es tema para otros posts.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.
P.S.: La imagen que ilustra el post tiene el correspondiente crédito al pie.
Inundaciones en la Provincia de Córdoba
 Con motivo de las inundaciones y anegamientos que están sucediendo en nuestra provincia, les he reunido en este post fuera de programa, bastante información de interés que he ido presentando a lo largo del tiempo en el blog.
Con motivo de las inundaciones y anegamientos que están sucediendo en nuestra provincia, les he reunido en este post fuera de programa, bastante información de interés que he ido presentando a lo largo del tiempo en el blog.
Sólo tienen que seguir los links que están más abajo para leer sobre cada tema. Pero les aclaro que son posts que subí hace mucho tiempo, de modo que la descripción de eventos específicos no corresponde al de hoy; sin embargo las explicaciones generales no han perdido vigencia en ningún caso.
- Alguna información sobre las inundaciones habituales en las Sierras Chicas
- Preguntas frecuentes sobre las inundaciones.
- ¿Era previsible que esto sucediera?
- Información sobre las precipitaciones intensas.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.
P.S.: La imagen que ilustra el postes de este sitio.
Otros lugares para turismo geológico. Parte 2
El lunes pasado subí la primera parte de este tema, y por ende deberían comenzar por leer ese post antes de internarse en éste.
En ese momento respondí a las siguientes preguntas:
¿En qué lugar se encuentran estos paisajes kársticos?
¿Qué origen reconoce la palabra karst?
¿Qué son los paisajes kársticos?
¿Cómo se produce la karstificación?
En esta parte 2, completaremos las restantes preguntas:
¿Cuál es el entorno geológico del Carso?
En general el Carso se encuentra en el contexto de los Alpes Dináricos constituidos mayoritariamente por materiales calcáreos mesozoicos, y enclavados en un área climáticamente favorable para la disolución lenta de esos materiales. Los Alpes Dináricos son una cadena montañosa que se extiende 645 km con dirección noroeste – sudeste, acompañando aproximadamente la costa del mar Adriático.
La cordillera se extiende 200 y 250 km en la dirección transversal, y ostenta alturas de entre 1.000 y 1.600 m, siendo su cumbre más alta, el Prokletije, situado en la frontera entre Montenegro y Albania. Sin embargo, toda la cadena toma el nombre de la monataña Dinara, situada entre Croacia y Bosnia-Herzegovina.
Durante el Cuaternario la zona estuvo intensamente modificada por glaciaciones recurrentes, que en algunos sitios han dejado paredes desnudas de toda vegetación, y de un blanco tan puro que se constituye en uno de sus tantos atractivos visuales.
¿Cuáles rasgos del relieve kárstico son particularmente atractivos para el turismo?
Como ya dije antes, los caracteres kársticos incluyen un amplio abanico y hablaremos de ellos en otro post, pero hoy nos abocaremos a los rasgos que atraen al turismo, y que son básicamente sus enormes cavernas, ocupadas o no por el agua, las grutas; y los laberintos subterráneos de cursos de agua que a veces tras largos periodos de socavamiento provocan la caída de los techos, generando grandes desfiladeros en los que vuelve a aflorar el agua.
La inmersión parcial de los Alpes Dináricos occidentales da origen a numerosas islas que corresponden a sus cimas emergidas, a lo largo de la costa croata.
¿Cuáles son las cavernas, grutas, y cuevas más conocidas?
Son más que numerosas, algunas más conocidas que otras, pero los circuitos turísticos suelen incluir una o más de las siguientes según cuál sea el recorrido seleccionado.
Cuevas de Skocjanske, Eslovenia.
Descubiertas en 1884, comprenden once cámaras interconectadas a lo largo de 6 km, con cascadas subterráneas, y un río, el Reka que fluye por abajo. Generalmente el turismo sólo visita la cámara Martelova de 123 m de ancho, 300 de largo y una altura de 146 metros.
Cuevas de Croacia. Son tan numerosas que para mejor organizar la información, las menciono por regiones, comenzando desde el extremo sur de la costa adriática.
Cuevas de la zona de Dubrovnik
- Cueva de Odiseo u Odisejeva Spilja, está ubicada en el sur de la isla de Mljet, y debe su nombre a una leyenda, según la cual fue el refugio de Odiseo cuando desató la furia de Poseidón. Se encuentra frente al acantilado Ogiran, y se accede a ella a través de un túnel de unos 20 m, que se recorre a nado o en diminutas barcas.
- Cueva de Vela Spilja, en Vela Luka, situada en la parte oeste de la isla de Korcula, sobre el monte Pinski Rat, a 130 msnm. Contiene un yacimiento arqueológico, y mide alrededor de 40 metros de longitud y 17 metros de altura.
Cuevas de la zona de Split Dalmacia, Croacia
- Cueva Azul, sita en la isla de Bisevo, en el Adriático, tiene como indica su nombre, aguas de un profundo color azul, a las que se accede solamente navegando.
- Cueva Mamet, está también en la misma isla, y tiene unos 200 metros de profundidad, con una entrada muy estrecha, que recién luego de recorrer aproximadamente 50 metros comienza a ensancharse creando una cuenca profunda con vistas espectaculares encerradas por paredes casi totalmente verticales.
- Cueva de Medvidina o Medvidina Spilja, también en la isla de Bisevo, en la porción sur, es supuestamente el hogar de la foca monje del Mediterráneo.
- Cueva del Dragón, ubicada en el sur de la isla de Brac, muestra paredes decoradas con símbolos paganos, relieves de animales y un gran dragón. Cuenta con protección para su conservación y sólo se puede visitar en excursiones organizadas por la Oficina de Turismo local.
Cuevas de la región de Zadar
- Cueva de Cerovacke, sita en el Parque Natural de Velebit, consta de 3 cuevas denominadas Donja, Srednja y Gornja, sumando más de 7 km de canales explorados con temperaturas que oscilan entre 5 y 8ºC.
- Cueva de Golubinka o Spilja Golubinka, se encuentra en la costa oeste de la isla de Dugi Otok o isla Larga, en la bahía de Brbinjscica, a la que se llega a nado o en una estrecha barquita.
Cueva en la Región de Lika.
- Cueva de Samograd, está en el Parque Grabovaca, y se accede a ella a través de unos escalones de piedra cincelados a mano hace más de cien años.
Cuevas de la Región de Istria, Croacia.
Probablemente es la zona más visitada, y exhibe, entre otras, las siguientes cuevas:
- Pazin, en la que se inspiró al mismísimo Julio Verne, y que se encuentra protegida. Sólo es posible visitarla con autorización de la Asociación de Espeleología de Istria. Tiene un sendero subterráneo de unos 200 metros de largo que termina en un lago subterráneo.
- Cueva de Baredine, con gran profusión de estalactitas, estalagmitas y esculturas subterráneas, es Monumento Natural desde 1995.
- Cueva Seagull´s Rocks (Rocas de las Gaviotas) se encuentra en la bahía de Muzilj, dentro de la península Stoja.
Ya alejados de la costa Adriática, en el interior del continente se encuentran las cuevas de Zagreb y de Kaprina, como las más importantes.
Cuevas en la región de Zagreb, Croacia.
- Cueva de Veternica, se encuentra a pocos kilómetros de la capital, en el Parque Nacional de Medvednica y es la sexta en tamaño de Croacia. Es hábitat de los murciélagos, por lo cual no puede visitarse en invierno cuando ellos están protegidos para su hibernación. Siendo un Monumento Geomorfológico de la Naturaleza, protegido desde 1979, no se permite el acceso más allá de los primeros 30 metros.
Cuevas de la región de Krapina.
Cueva de Vindija y Cueva de Krapina, ambas son yacimientos paleontológicos de suma importancia para Europa.
¿Qué puede agregarse?
Por fuera del interés esencialmente turístico, geomorfológico y espeleológico, las cuevas albergan una fauna troglodita que es digna de estudio y preservación.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.
P.S.: La imagen que ilustra el post corresponde a las cavernas Skocian de Lipica en Eslovenia, y la he tomado de este sitio.
