Isostasia. Parte 1
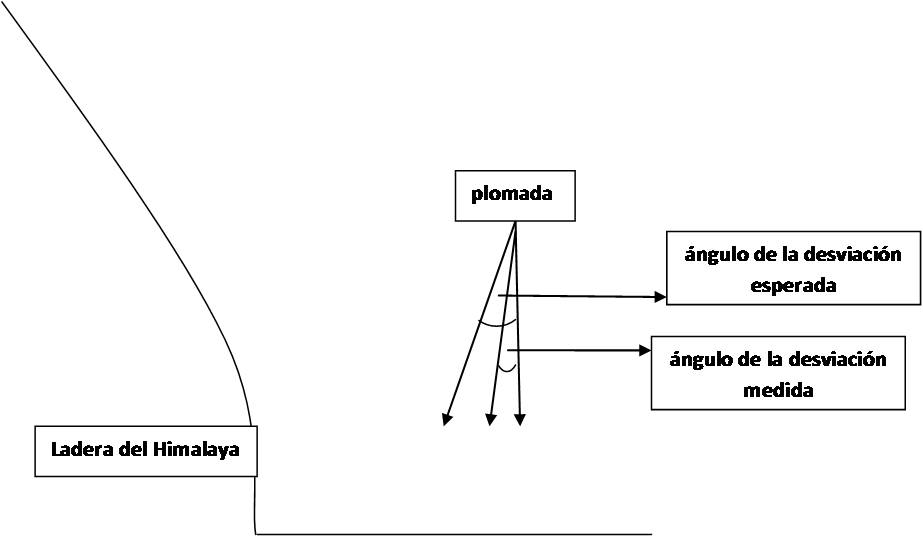
Esquema teórico, en el que no se ha respetado escala alguna. Imaginen si no, ¡qué pedazo de plomada deberían haber transportado esos estudiosos!
Hoy comenzaremos a tratar un tema que es sustancial para la comprensión cabal de toda la Tectónica Global o de Placas, como también se la conoce. Por eso iremos pasito a paso, y lo veremos en tres partes, a subir en tres semanas consecutivas.
Hoy contestaré las primeras y más básicas preguntas, a saber:
¿Qué movimientos de gran extensión areal explica la isostasia?
En un post no muy lejano les expliqué que la arquitectura terrestre responde en gran medida a porcesos de enorme extensión areal que pueden agruparse esencialmente en dos grupos bien diferenciados- aunque en ese post les expliqué otros dos grupos más, de menor relevancia- a los que se conoce como orogénicos y epirogénicos. Pues bien, la isostasia es la principal responsable de estos últimos, que tienen una dirección de desplazamiento radial respecto al esferoide terrestre. Les recomiendo repasar ese post.
¿Qué se entiende por isostasia?
La palabra isostasia procede de dos vocables griegos: Isos, que significa igual, y stásis, que indica paralización o inmovilidad, lo que nos lleva a reconstruir el significado como «permanecer igual», remitiéndonos a una condición de equilibrio.
En una primera aproximación, que se irá ajustando a medida que comprendamos todos los fundamentos del proceso, puede decirse que la isostasia es la tendencia de todas las grandes masas de la corteza terrestre, y de parte del manto superior a alcanzar una posición de equilibrio gravitacional dinámico, fluctuante y autoregulado, respecto a las masas circundantes. Por supuesto, los ajustes se producen a lo largo de cientos, miles o millones de años. No debemos pensarlos como respuestas inmediatas, sino muy graduales.
¿Cómo se reconoció la ocurrencia de este proceso?
Hacia 1735, Pierre Bouguer realizó una expedición científica a los Andes de Perú, y realizó mediciones en las que observó que la desviación que respecto a la vertical inducía sobre una plomada la masa montañosa, era bastante menor que la esperada. El fenómeno llamó su atención como para relatarlo en sus memorias de viaje, y fue nuevamente observado por Sir George Everest un siglo más tarde en 1840.
En ese momento, se buscó una explicación científica y para ello se aplicó la ley de la gravedad, pues ya era sabido que la plomada sería atraída por la masa montañosa. Lo que debía explicarse era por qué el cálculo teórico de la atracción esperada- manifestada en el ángulo de desviación de la plomada que pueden ver en el dibujo- era hasta tres veces mayor que el resultante del ángulo de desviación real medido en el campo.
Considerando que ya los métodos de cubicación, afinados en la minería, permitían un cálculo bastante aproximado del volumen del cuerpo montañoso involucrado, bastaba con analizar la fórmula básica de la atracción gravitatoria, para buscar por dónde se introducía el error en el resultado obtenido. En un post anterior les he explicado el tema de la ley de la gravedad en detalle, pero recordemos que la expresión matemática de la Fuerza de atracción gravitacional es:
F= G m.m’/ r2
Donde:
F= fuerza de atracción de la Gravedad.
G= es un valor constante y conocido.
m y m’= son las dos masas involucradas en este fenómeno de atracción. En nuestro caso, la plomada y el monte aledaño.
r = es la distancia que separa a las masas en cuestión, perfectamente medida en el experimento.
Obviamente, el ángulo medido responde directamente a la fuerza de atracción ejercida, en este caso por la masa montañosa, es decir que el resultado inesperado se debe a alguna medición también errónea de los elementos de la fórmula. Pero sucede que todos son valores perfectamente conocidos. En efecto, G es constante; la masa de la plomada es fácilmente determinada, y la distancia desde la ladera, sólo puede incluir errores muy pequeños, a menos que uno sea muy nabo.
Pero… y ahí está¡ el quid de la cuestión, la masa de la montaña se calcula a partir de su volumen que es medido por métodos tradicionales. Y sabemos que:
Densidad= masa /volumen.
o lo que es lo mismo,
masa (m) = volumen por densidad. ¡et voilá!
Si no somos tontos, sabemos calcular el volumen, de modo que el único error que puede explicar por qué la montaña atrae menos de lo esperado a la plomada, es porque su masa es más pequeña de lo calculado, y ¿por culpa de quién? Pues de la densidad que es menos de la que se había considerado en el esquema teórico original.
En otras palabras, el misterio ahora a explicar es de dónde sale ese déficit de densidad. ¿Les va gustando esta novelita de suspenso?
Pues entonces, si quieren conocer el desenlace, recuerden que hasta aquí será¡ el tema de hoy, y retomaremos en la semana próxima respondiendo las siguientes preguntas:
¿Qué teorías surgieron inicialmente para explicar el déficit de densidad que se estableció empíricamente?
¿Cuál de estas teorías sobrevive, y cómo se la puede explicar de manera sencilla?
¿Qué modificación se introdujo más tarde?
En el tercer post se verán los siguientes tópicos:
¿Puede demostrarse la teoría de Airy mediante cálculos reales?
¿Cómo pueden sintetizarse los conceptos básicos de la isostasia?
¿Qué consecuencias tiene la isostasia en la estructura general y la dinámica de la Tierra?
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.
Genial la manera como explicas.
Felicitaciones.
Muchas gracias, Gustavo.
Muchas gracias Graciela y equipo es una excelente pagina, me encantó !!! me estoy por recibir de profe de geografía. Me ayudas mucho con estos conceptos! tenes instagram?
muchas gracias bendiciones
Hola, ABY. Gracias por tus conceptos. Sí tengo IG, es gracielal.arguello, aunque le presto poca atención porque no me gusta la restricción de tiempo de visualización y de espacio para escribir. Sigo estando más activa en FB. Y pos supuesto en este blog y el otro (¿Y si hubiera una vez?) que te invito a conocer, ya que es de un carácter muy distinto, sobre la base de mi actividad como escritora no sólo científica sino también de humor y ficción. Un abrazo Graciela.