Locos por la Geología

Archivo de la categoría ‘Geología para principiantes’

Este tema es de por sí complejo y extenso, de modo que empiezo por presentarles una síntesis apretada y sencilla, y a lo largo del tiempo profundizaremos lentamente en aspectos particularmente interesantes.

Aun así, habrá que dividir este tema en dos posts, el primero de los cuales es éste y el segundo subirá el próximo lunes.

El objetivo de hoy es esencialmente comprender cómo se distribuyen sobre todo el planeta, el calor disponible y la temperatura resultante.

Todavía no les he contado mucho sobre la atmósfera, de modo que tendrán que aceptar algunas cosas como válidas, aun antes de que se las explique en detalle, cosa que haré en un post específico más adelante.

¿Qué procesos intervienen en la circulación atmosférica?

Los principales procesos que debemos comprender para seguir este post son separados para su mejor comprensión, pero la distinción es más bien teórica, ya que en los hechos, todos se interrelacionan muy estrechamente y ocurren muchas veces simultáneamente.

Esos procesos teóricos. que ya les he explicado en otro post y por ende deben ir a repasar allí, son:

• Advección.
• Fuerza y efecto de Coriolis, que veremos muy detalladamente más adelante en futuros posts del blog, pero del cual ya les he adelantado algo en este post.
• Convección.
• Procesos y efectos adiabáticos.

¿Qué se entiende por centros ciclónicos y centros anticiclónicos?

Si bien  l.s. centro ciclónico y ciclón son sinónimos, los meteorólogos suelen reservar el término ciclón para referirse a vientos intensos acompañados de tormenta, por eso prefiero en este momento usar la expresión compuesta (centro ciclónico) para evitar confusiones.

Mucho les he adelantado ya sobre este tema en el post que he linkeado un poquito más arriba, de modo que deberían ir a leer esos conceptos allí.

Aquí agregaremos que la formación de un sistema de baja presión (centro ciclónico) se denomina ciclogénesis y que el sistema que así se genera se caracteriza por movimientos divergentes en altura, compensados por movimientos de ascenso, que dejan un espacio en los niveles inferiores, al que acuden corrientes de aire convergentes al nivel del suelo.

El efecto opuesto genera centros anticiclónicos o de alta presión, en los que el aire converge en niveles altos, causando un descenso o subsidencia vertical, y la consiguiente divergencia a nivel de la superficie terrestre.

Un anticiclón es normalmente responsable de tiempo estable y ausencia de precipitaciones, ya que la subsidencia limita la formación de nubes. Lo opuesto se cumple en los centros de baja presión o centros ciclónicos. En cada caso, la presión atmosférica de cada tipo de centro, es mayor o menor respecto al aire circundante, pero no requiere valores definidos.

Los ciclones y anticiclones tienen un rol fundamental en la dinámica de los vientos o corrientes y de la circulación atmosférica planetaria. En general, un centro ciclónico (de bajas presiones) atrae masas de aire atmosférico desde las zonas de altas presiones o anticiclónicas.

¿Cómo se intentó por primera vez explicar la circulación atmosférica planetaria?

El primer ambicioso intento de esclarecer este punto data de 1735, cuando el meteorólogo inglés George Hadley presentó un modelo de circulación de una celda de gran extensión, en la que el aire cálido asciende en el ecuador y desciende en los polos según un proceso de convección directa, tal como se ve en la figura que ilustra el post.

Esta teoría tiene el mérito de ser una explicación coherente para la redistribución de la energía solar en el planeta, y de ser compatible con algunas realidades observadas, tales como las diferencias térmicas a lo largo de los cambios latitudinales, desde el ecuador donde los rayos solares inciden normalmente a la superficie, hasta los polos donde esa incidencia tiene la mayor oblicuidad.

¿Por qué no fue suficiente esa explicación?

Por varias razones: en primer lugar una celda tan sencilla supone una Tierra uniformemente cubierta de agua, donde la distribución del calor es bastante homogénea. En un planeta en que parte de las superficie es acuática, con elevado calor específico, y otra parte incluye materiales sólidos donde ese valor es altamente variable, el calentamiento sigue un patrón mucho más complejo que el establecido por Hadley.

Por otra parte, en el modelo de celda única no se considera la rotación del planeta, y su importante consecuencia: la fuerza de Coriolis, por lo cual no explica del todo la distribución real de los vientos, que se observa en el planeta.

Por hoy es suficiente, en el post de la semana próxima veremos los siguientes temas.

¿Qué nuevo modelo surgió luego del de una celda?

¿Qué es la zona de convergencia intertropical?

¿Qué son las corrientes en chorro o jet?

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La imagen que ilustra el post fue tomada de un curso de divulgación sobre «Eventos climáticos a escala global», cuyo autor es Horacio Sarochar, y fue publicado por la Secretaría de Difusión de la Facultad de Ciencias Astronómicas y Geofísicas de la Universidad Nacional de La Plata.

Ustedes han venido siguiendo conmigo el advenimiento de mi bebé dinosaurio (que todavía no tiene nombre, porque estoy esperando sus sugerencias), y les prometí que una vez que estuviera bien presentable, les explicaría algo sobre la especie que representa. O que creo que representa, porque al fin y al cabo no es más que un juguete, y la clasificación, por eso mismo, nunca es cien por ciento segura.

Les parecerá una aclaración tonta, pero no faltó el desubicado que se puso a discutir la taxonomía de Sid, el dibujito animado de la Era del Hielo. ¡Imagínense!

¿Qué dinosaurio estaría mi juguete representando?

Observando mi juguete, vienen a mi memoria algunas posibilidades, nunca muy distantes entre sí, y tengo que decidirme por una, simplemente mirando sus rasgos más sobresalientes, cosa que no responde en absoluto a las técnicas científicas que se aplican para una verdadera clasificación.

Por eso, elegir un nombre es en este caso, sobre todo un juego y una excusa para ponerlos a ustedes, chicos, en contacto con algunas nociones sobre un dinosaurio en particular.

Así pues, el dinosaurio que a mi modo de ver más se parece a mi «mascotita» es el Saurolophus, del que hablaremos en este post.

¿Por qué características supongo que lo es?

Mirando el juguete, las características que saltan a la vista son:

• la desproporción entre las extremidades anteriores y las posteriores, relacionada con una forma de cadera que lo ubica en el orden Ornistichia (ya hablaremos en otro post de esto, porque es muy interesante)
• la cresta sobresaliente,
• la fuerte cola,
• el hocico semejante a un pico de pato.

Por supuesto que todos esos rasgos están suavizados por razones de fabricación y para hacer del animalito un juguete más simpático. Pero tomándolos todos en conjunto, creo que decidirme por un Saurolophus no estaría lejos de la intención del fabricante (que no le ha puesto nombre científico alguno en las especificaciones).

¿Cómo es su clasificación completa?

Este animal se clasifica como sigue:
Reino: Animalia
Filo: Chordata
Clase: Sauropsida
Superorden: Dinosauria
Orden: Ornithischia
Suborden: Neornithischia
Infraorden: Ornithopoda
Familia: Hadrosauridae
Subfamilia: Saurolophinae
Tribu: Saurolophini
Género: Saurolophus
Especies descritas:

Saurolophus osborni
Saurolophus angustirostris

Conviene señalar que hay menciones de al menos una posible especie más, pero hay al respecto todavía mucha discusión, por lo cual, su inclusión en la taxonomía es muy dudosa, y yo prefiero esperar antes de hacerlo.

De estas dos especies aceptadas, la osborni residía en América, y por tratarse de un juguete yanqui, asumo que es la representada por mi bichito. La angustirostris era asiática, en cambio.

¿De qué tamaño habría sido en la realidad?

Como ya dije más arriba, estoy asumiendo (un poco caprichosamente) que mi mascota es Saurolophus osborni, de modo que habría medido casi diez metros de largo, y pesado casi dos toneladas. Su cráneo era de aproximadamente un metro.

Si se tratara de la otra especie, habría sido todavía más grande.

¿De dónde deriva su nombre y quién lo descubrió?

La palabra se compone a partir de dos términos griegos: sauro= lagarto y lophus= cresta; con lo que se apunta a su más notable característica morfológica. (Les recuerdo, chicos, que morfología significa «estudio de las formas», y no tiene nada que ver con comer mucho).

El primer hallazgo de restos fósiles de Saurolophus se debe a Barnum Brown y data de 1911.

Se trató de un hallazgo afortunado porque era un esqueleto casi completo- lo cual no es para nada común- que hoy puede verse en el Museo Americano de Historia Natural.

Brown lo encontró en Canadá, más específicamente en sedimentos del Cretácico Superior de la Formación Cañón Herradura, (que en el tiempo de las excavaciones de Brown tenía otro nombre) y que se ubica en el Río Deer, en Alberta.

¿Para qué habría servido su cresta?

No hay acuerdo absoluto entre los científicos al respecto, pero se le atribuyen funciones tan variadas como:

• facilitar la respiración,
• regular la temperatura,
• ser un ornamento para atraer ejemplares con los que aparearse,
• servir para emitir sonidos de comunicación.

En un principio, cuando se pensaba que era completamente sólida, también se la pensó como un rudimentario elemento defensivo, idea que se desestimó al comprobarse que en realidad contenía numerosos canales huecos, que por un lado la hacían más frágil para esa función, y por el otro, apuntaban mejor a cualquiera de las utilidades mencionadas en la lista anterior. Probablemente cumplía dos o más de esas funciones simultáneamente.

¿Dónde y cuándo vivió?

Según los registros con que se cuenta, habría vivido en el Cretácico tardío, vale decir hacia fines de la Era Mesozoica, más específicamente hace entre 74 y 70 millones de años atrás.

Su distribución geográfica habría sido en los territorios que hoy corresponden a Canadá y Asia del norte.

¿Cómo habrían sido sus hábitos?

Según la interpretación de los fósiles que se han recuperado, los Saurolophus podían moverse tanto sobre sus cuatro patas, como solamente sobre las traseras y elevando el tronco, lo que les permitía alimentarse- siendo herbívoros- de plantas hasta una altura de aproximadamente cuatro metros.

En otras palabras, tenían dos alternativas de locomoción: como bípedos y como cuadrúpedos. La posición de cuadripedia era probablemente la utilizada para correr, mientras que la bípeda era la preferida a la hora de alimentarse de hojas a gran altura.

Debido a que no han podido identificarse en los registros fósiles, órganos específicos de su cuerpo que les permitieran una defensa muy efectiva frente a posibles depredadores, se supone que se reunían en pequeñas manadas para obtener una mejor protección.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

P.S.: La imagen que ven más abajo es de wikipedia, mientras que las fotos, obviamente son mías. Pero no de mi persona, sino de mi juguete, 😀

De Debivort – English Wikipedia, image was slightly altered., CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2195622

Un abrazo y hasta el miércoles. Graciela.

Gracias a los buenos oficios de mi colega, Marcelo Dalponte, ha llegado a mis manos, para compartir con ustedes, la cartilla de alertas volcánicas del Sernageomin (Servicio Geológico Minero chileno), que ilustra el post y que les recomiendo ver en detalle.

De paso les cuento un poco sobre el volcán Copahue que hoy se encuentra en alerta amarilla.

¿Dónde queda el volcán Copahue?

El volcán Copahue se encuentra en la zona limítrofe entre Chile y Argentina, afectada por la dinámica de contacto entre las placas Sudamericana y de Nazca, que como ya he explicado otras veces implica una subducción responsable tanto de actividad sísmica como volcánica, ambas muy habituales e intensas.

El nombre del volcán se origina en la lengua mapuche, en la cual ko, significa «agua»; pa, designa al «azufre»; y we, quiere decir «lugar». En definitiva, Copahue es «el lugar de las aguas sulfurosas», en clara alusión a las aguas termales de la zona.

¿Qué tipo de volcán es, y cuándo se han registrado las erupciones más recientes?

Se trata de un estratovolcán activo, con numerosas erupciones recientes, entre las que se pueden mencionar las de 2012, 2013, 2014 y 2015, ninguna de las cuales superó la alerta naranja, ya que casi siempre se trató de emisiones de columnas de materiales muy finos expulsados sin excesiva violencia y a gran altura. Siempre estuvieron precedidas por enjambres sísmicos de intensidad entre 2 y 4 o 5 grados Mercali.

¿Qué más puede decirse de este volcán?

Lo más importante, es que genera permanentemente fenómenos conocidos como «postvolcánicos», del tipo de las fumarolas, lo que da lugar a la explotación turística de sus fuentes de aguas termales, en la zona circundante al Lago Caviahue, y en la localidad de Copahue, aprovechamiento que tiene ya más de 100 años.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

Hoy vamos a retomar las propiedades minerales que se aprecian a simple vista, y con  maniobras muy simples. Particularmente seguiremos con el sistema cristalino, que como verán en el cuadro, es una de las características que dependen del estado de agregación.

Para entender este post, conviene que lean antes otro post en el que les expliqué qué es el estado cristalino.

No dejen de repasar esos conceptos, porque todo lo dicho en ese post lo doy por conocido y no lo repetiré aquí.

¿Cuántos y cuáles son los sistemas cristalinos?

Son siete, aunque en alguna bibliografía antigua el sistema trigonal se definía de manera ligeramente diferente y muchos lo consideraban dentro del hexagonal, como caso particular. De allí que a veces encuentren un listado de sólo seis sistemas.

Conviene señalar que los sistemas presentan además variaciones internas, que permiten su subdivisión en 32 clases, y las formas cristalinas posibles son todavía muchas más.

Los sistemas que hoy reconocemos son:

1. Cúbico.
2. Rómbico.
3. Tetragonal.
4. Hexagonal.
5. Romboédrico o trigonal.
6. Monoclínico.
7. Triclínico.

¿Cómo se los reconoce?

La manera de definir un sistema cristalino es según los ejes cristalográficos presentes en el cristal, y los ángulos que se definen entre esos ejes.

No se deben confundir los ejes de simetría con los cristalográficos, porque sólo algunos de ellos coinciden entre sí.

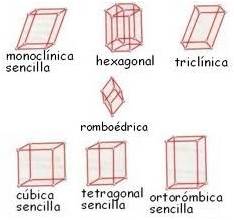
figura 1

¿Cuáles son los elementos de simetría?

Hay planos, ejes y centros, y en algunos casos, repito, ciertos ejes de simetría coinciden con los cristalográficos.

Pero del tema simetría y sus elementos no hablaremos en este post, sino en otros a subir en el futuro, porque de no separar los temas, podríamos generar alguna oscuridad en los conceptos básicos.

¿Qué son los ejes cristalográficos?

Los ejes cristalográficos se definen de manera tridimensional, y corresponden a líneas rectas imaginarias que atraviesan el centro del cristal y definen allí lo que se conoce como cruz axial. Se eligen de preferencia de manera tal que sean paralelos a aristas de cristales reales, para poder visualizar mejor la cruz axial. Pueden ser tres o cuatro, según sea el sistema en cuestión. (Ver figura 2)

Cuando todos los ejes son perpendiculares entre sí, los sistemas cristalográficos se conocen como ortogonales. Es el caso de los sistemas cúbico, rómbico y tetragonal.

Cuando alguno o algunos de los ángulos de la cruz axial no son rectos, las redes cristalinas son no ortogonales, categoría que comprende los sistemas hexagonal, trigonal, monoclínico y triclínico.

Debemos tener presente que en la posición convencional de «lectura» de un cristal, el eje cristalográfico que va de adelante hacia atrás se denomina eje a, el b va de derecha a izquierda y el c desde arriba hacia abajo.

Si los ejes son desiguales, casi siempre el c es el más largo.

Cuando hay un cuarto eje, tres se cortan en el plano horizontal, según 120° hasta completar los 360 de la circunferencia completa. Obviamente, encontraremos un semieje horizontal cada 60° en el giro completo. El restante eje será siempre el c, y su posición es vertical.

¿Cómo se reconoce el sistema cúbico?

Se conoce también como isométrico y puede decirse de él que es monométrico, ya que los tres ejes cristalográficos son todos de igual longitud, es decir que hay una sola medida tres veces repetida. (Ver figura 1). Todos los ejes se cortan en ángulos rectos (90°).

Algo digno de destacar es que es el único sistema isotrópo, vale decir que tiene las propiedades vectoriales idénticas en todas las direcciones, ya que se inscribe bien en una esfera perfecta.

¿Cómo se reconoce el sistema rómbico u ortorrómbico?

Presenta tres ejes, todos en ángulo recto, con longitudes diferentes entre sí.

¿Cómo se reconoce el sistema tetragonal?

Tiene los tres ejes, todos en ángulo recto, dos de ellos con igual longitud (a y b) y uno (c) de diferente medida.

¿Cómo se reconoce el sistema hexagonal?

Es uno de los dos que tiene cuatro ejes, dispuestos como he explicado más arriba, es decir que tres de los ejes son horizontales y contenidos en el mismo plano, además de exhibir la misma longitud. El cuarto eje, el c, es de diferente longitud, y pasa a través de la intersección de los otros ejes en ángulo recto con el plano que los contiene.

¿Cómo se reconoce el sistema trigonal o romboédrico?

En general la relación de los ejes cristalográficos y de los ángulos entre ellos es semejante a la del hexagonal, pero carece de plano de simetría horizontal, vale decir que no se repite la misma forma arriba que abajo del plano central que ocupa la posición horizontal. Por ejemplo, arriba puede haber una cara y abajo un vértice en la misma posición.

¿Cómo se reconoce el sistema monoclínico?

En este sistema, los tres ejes son todos desiguales en longitud, dos de los cuales se cortan en ángulo recto, y el tercero corta al plano entre ellos con un ángulo oblícuo.

¿Cómo se reconoce el sistema triclínico?

Tiene tres ejes, todos desiguales en longitud y que se cortan según tres ángulos diferentes entre sí y distintos de 90°.

¿Qué más se debe considerar con respecto a este tema?

Es importante tener en cuenta algunos aspectos complementarios. En primer lugar, si bien los minerales de una especie dada, siempre cristalizan en el mismo sistema, por lo cual podría considerarse que esta característica es una propiedad diagnóstica, no siempre puede usarse, porque a veces el tamaño del cristal es tan pequeño que no se observa a simple vista.

Además, cada sistema, como dije más arriba, presenta variaciones y las formas cristalinas resultan muchas veces de facetados o intercrecimientos que dan formas muy complejas y difíciles de describir en minerales reales.

Esto último es así, porque la expresión final depende de parámetros externos y variables, como el espacio y material disponibles durante el crecimiento. Así, por ejemplo, si numerosos cristales se van formando simultáneamente en un espacio pequeño, la competencia entre ellos puede hacer que se deformen unos a otros, dando formas incompletas o contorsionadas.

Un ejemplo particularmente interesante es el caso de las maclas (cristales que crecen juntos como siameses, digamos) y que veremos en otra oportunidad.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.

P.S.: La imagen de la figura 1 es de este sitio. A la figura 2, la tomé de aquí.

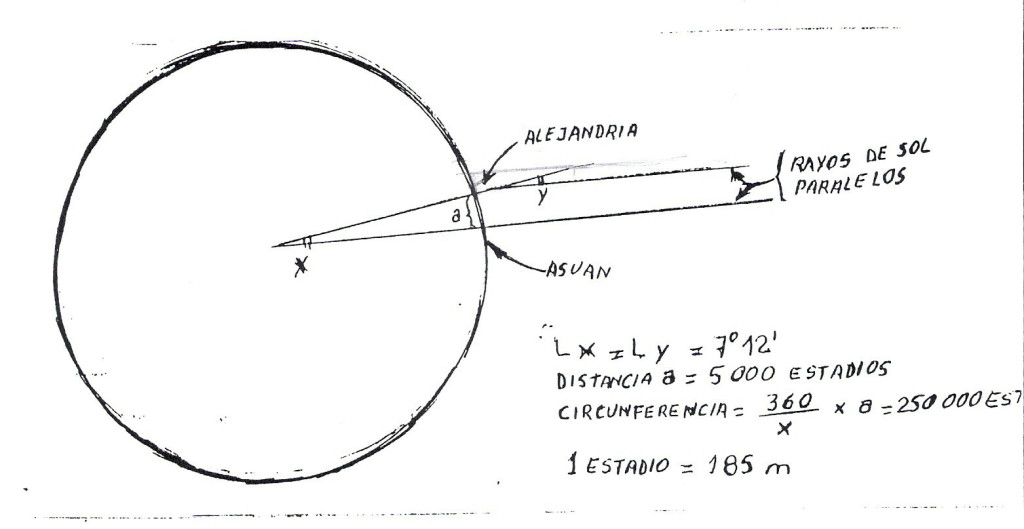
Figura 1

Este post es continuación del de la semana pasada, de modo que deberían empezar por leerlo antes de internarse en el de hoy.

El lunes pasado respondí las siguientes preguntas:

¿Cuáles son las dimensiones más significativas de la Tierra?

¿Qué es un arco de meridiano?

¿Para qué sirve conocer la longitud del arco de meridiano?

¿Quién midió el arco de meridiano por primera vez?

¿Quién fue Eratóstenes?

A partir de aquí, retomamos las preguntas que quedaron pendientes en la primera parte de este post, que publiqué el lunes pasado:

¿Cómo se dio cuenta de que la Tierra era redonda y que podpia medir su circunferencia?

En primer lugar, recordemos que los griegos ya sabían de la esfericidad de la Tierra desde el Siglo V antes de Cristo, en función de observaciones que ya les he comentado antes, pero en el caso particular de Eratóstenes, las pruebas de que se valió fueron relativamente sencillas.

Siendo director de la Biblioteca de Alejandría, Eratóstenes tenía acceso a información muy calificada para la época, y en uno de los tantos papiros en los que esa información se registraba, leyó que en la ciudad de Siena, (hoy llamada Assuán y situada unos 800 km al sureste de Alejandría) los rayos solares al caer sobre una vara el mediodía del solsticio de verano (el actual 21 de junio) no producían sombra alguna.

Picado por la curiosidad, Eratóstenes comenzó a replicar esas observaciones en Alejandría, utilizando la iluminación en un pozo, que era completa siempre en un mismo día y a la misma hora, y se desplazaba, en cambio, dejando parte del pozo en sombras en cualquier otro momento.

No obstante, las horas de sombra cero no coincidían en los registros de ambas ciudades. Ahora bien, asumiendo, muy correctamente que si el Sol se encuentra a una distancia tan grande que es comparativamente infinita respecto a las consignadas en la Tierra, sus rayos son paralelos, ya que se reúnen precisamente en el infinito.

El sabio coninuó un paso más adelante, razonando que si los rayos solares son paralelos, al alcanzar una Tierra plana, como algunos todavía insistían por entonces, no debería haber diferencias entre las sombras proyectadas por los objetos a la misma hora del mismo día, independientemente de la distancia entre ellos. Las diferencias en las sombras sólo podían explicarse sobre una superficie curva, tal como se ve en la Figura 2.

Con esos mismos juegos de distancias y sombras, midió el arco de meridiano que le serviría para establecer en seguida la circunferencia de la Tierra, tal como les expliqué el lunes pasado.

Figura 2

¿Cómo formuló la medición del arco de meridiano?

Con esas observaciones previas como dato inicial, Eratóstenes se valió del razonamiento que les muestro en la Figura 1, para medir el arco de meridiano (a en ese dibujo).

Como pueden ver en el diagrama, los rayos solares, considerados paralelos definen en Siena sombra cero para una estaca, pero en Alejandría, arrojan una sombra con una estaca (que al estar vertical sería como una continuación del radio terrestre), y forman con esa estaca un á¡ngulo ( denominado y en el dibujo), que resulta igual al ángulo interno de la Tierra (x del dibujo) que subtiende al arco a entre Siena y Alejandría, cuya longitud pretendía medir.

Los ángulos x e y son iguales, precisamente porque son ángulos correspondientes entre paralelas, y un teorema ya existente había demostrado ese postulado.

En definitiva, para conocer el valor de x, bastaba con medir y. Grande es la tentación de asumir que Eratóstenes se valió de la resolución trigonométrica del triángulo rectángulo entre los rayos, la estaca y su sombra…pero no. No se conocían los valores trigonométricos por entonces, de modo que utilizó un antiguo aparato denominado gnomon, y logró el valor de 7° 12′ para el ángulo y, exactamente igual a x.

Lo que siguió fue medir la distancia entre Siena y Alejandría, lo cual no se sabe exactamente cómo se realizó, tal vez contratando uno o más esclavos, como es la teoría más elegida; o encargando la cuenta a tropas que marchaban entre ambas ciudades, o a caravanas comerciales. Cualquiera haya sido el modo, Eratóstenes conoció también la distancia a, medida en estadios, como era lo normal en la época.

Con los valores de x y a ya en la bolsa, sólo tuvo que aplicar la fórmula que les puse en el dibujo, y que les expliqué la semana pasada, para conocer el perímetro de la cicunferencia terrestre.

¿Qué valor obtuvo?

Eratóstenes obtuvo un valor de aproximdamente 250.000 estadios, siendo la medida del estadio de 185 m. En definitiva, trasladando ese valor a las medidas actuales, el resultado es de 46.250 km.

¿Cuál es el valor que hoy consideramos el más preciso para la circunferencia de la Tierra?

Hoy se redondea y promedia el valor del perímetro de la circunferencia terrestre en 40.000 km, lo cual, si se considera la diferencia sideral entre los aparatos y métodos usados, asombra por su bajo error comparativo.

Como un plus más a la admiración que Eratóstenes nos provoca, es bueno recordar que él continuó por muchos años midiendo otros arcos de meridiano, y al encontrar variaciones significativas entre sus resultados, fue uno de los primeros en sugerir que la forma de la Tierra no era la de una esfera perfecta. En efecto, en una esfera perfecta, todos los ángulos iguales subtienden arcos iguales, cosa que no se reflejaba en sus calculos.

Para confirmar esta apreciación habrían de transcurrir por lo menos diecinueve siglos, pero eso ya es tema para otros posts.

Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.

Un abrazo y hasta el miércoles. Graciela.