Propiedades minerales: el sistema cristalino.
5 de junio de 2017 | 
Autor: 
Hoy vamos a retomar las propiedades minerales que se aprecian a simple vista, y con maniobras muy simples. Particularmente seguiremos con el sistema cristalino, que como verán en el cuadro, es una de las características que dependen del estado de agregación.
Para entender este post, conviene que lean antes otro post en el que les expliqué qué es el estado cristalino.
No dejen de repasar esos conceptos, porque todo lo dicho en ese post lo doy por conocido y no lo repetiré aquí.
¿Cuántos y cuáles son los sistemas cristalinos?
Son siete, aunque en alguna bibliografía antigua el sistema trigonal se definía de manera ligeramente diferente y muchos lo consideraban dentro del hexagonal, como caso particular. De allí que a veces encuentren un listado de sólo seis sistemas.
Conviene señalar que los sistemas presentan además variaciones internas, que permiten su subdivisión en 32 clases, y las formas cristalinas posibles son todavía muchas más.
Los sistemas que hoy reconocemos son:
- Cúbico.
- Rómbico.
- Tetragonal.
- Hexagonal.
- Romboédrico o trigonal.
- Monoclínico.
- Triclínico.
¿Cómo se los reconoce?
La manera de definir un sistema cristalino es según los ejes cristalográficos presentes en el cristal, y los ángulos que se definen entre esos ejes.
No se deben confundir los ejes de simetría con los cristalográficos, porque sólo algunos de ellos coinciden entre sí.
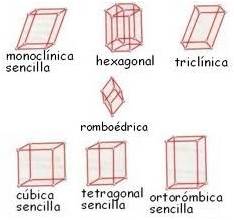
figura 1
¿Cuáles son los elementos de simetría?
Hay planos, ejes y centros, y en algunos casos, repito, ciertos ejes de simetría coinciden con los cristalográficos.
Pero del tema simetría y sus elementos no hablaremos en este post, sino en otros a subir en el futuro, porque de no separar los temas, podríamos generar alguna oscuridad en los conceptos básicos.
¿Qué son los ejes cristalográficos?
Los ejes cristalográficos se definen de manera tridimensional, y corresponden a líneas rectas imaginarias que atraviesan el centro del cristal y definen allí lo que se conoce como cruz axial. Se eligen de preferencia de manera tal que sean paralelos a aristas de cristales reales, para poder visualizar mejor la cruz axial. Pueden ser tres o cuatro, según sea el sistema en cuestión. (Ver figura 2)
Cuando todos los ejes son perpendiculares entre sí, los sistemas cristalográficos se conocen como ortogonales. Es el caso de los sistemas cúbico, rómbico y tetragonal.
Cuando alguno o algunos de los ángulos de la cruz axial no son rectos, las redes cristalinas son no ortogonales, categoría que comprende los sistemas hexagonal, trigonal, monoclínico y triclínico.
Debemos tener presente que en la posición convencional de «lectura» de un cristal, el eje cristalográfico que va de adelante hacia atrás se denomina eje a, el b va de derecha a izquierda y el c desde arriba hacia abajo.
Si los ejes son desiguales, casi siempre el c es el más largo.
Cuando hay un cuarto eje, tres se cortan en el plano horizontal, según 120° hasta completar los 360 de la circunferencia completa. Obviamente, encontraremos un semieje horizontal cada 60° en el giro completo. El restante eje será siempre el c, y su posición es vertical.
¿Cómo se reconoce el sistema cúbico?
Se conoce también como isométrico y puede decirse de él que es monométrico, ya que los tres ejes cristalográficos son todos de igual longitud, es decir que hay una sola medida tres veces repetida. (Ver figura 1). Todos los ejes se cortan en ángulos rectos (90°).
Algo digno de destacar es que es el único sistema isotrópo, vale decir que tiene las propiedades vectoriales idénticas en todas las direcciones, ya que se inscribe bien en una esfera perfecta.
¿Cómo se reconoce el sistema rómbico u ortorrómbico?
Presenta tres ejes, todos en ángulo recto, con longitudes diferentes entre sí.
¿Cómo se reconoce el sistema tetragonal?
Tiene los tres ejes, todos en ángulo recto, dos de ellos con igual longitud (a y b) y uno (c) de diferente medida.
¿Cómo se reconoce el sistema hexagonal?
Es uno de los dos que tiene cuatro ejes, dispuestos como he explicado más arriba, es decir que tres de los ejes son horizontales y contenidos en el mismo plano, además de exhibir la misma longitud. El cuarto eje, el c, es de diferente longitud, y pasa a través de la intersección de los otros ejes en ángulo recto con el plano que los contiene.
¿Cómo se reconoce el sistema trigonal o romboédrico?
En general la relación de los ejes cristalográficos y de los ángulos entre ellos es semejante a la del hexagonal, pero carece de plano de simetría horizontal, vale decir que no se repite la misma forma arriba que abajo del plano central que ocupa la posición horizontal. Por ejemplo, arriba puede haber una cara y abajo un vértice en la misma posición.
¿Cómo se reconoce el sistema monoclínico?
En este sistema, los tres ejes son todos desiguales en longitud, dos de los cuales se cortan en ángulo recto, y el tercero corta al plano entre ellos con un ángulo oblícuo.
¿Cómo se reconoce el sistema triclínico?
Tiene tres ejes, todos desiguales en longitud y que se cortan según tres ángulos diferentes entre sí y distintos de 90°.
¿Qué más se debe considerar con respecto a este tema?
Es importante tener en cuenta algunos aspectos complementarios. En primer lugar, si bien los minerales de una especie dada, siempre cristalizan en el mismo sistema, por lo cual podría considerarse que esta característica es una propiedad diagnóstica, no siempre puede usarse, porque a veces el tamaño del cristal es tan pequeño que no se observa a simple vista.
Además, cada sistema, como dije más arriba, presenta variaciones y las formas cristalinas resultan muchas veces de facetados o intercrecimientos que dan formas muy complejas y difíciles de describir en minerales reales.
Esto último es así, porque la expresión final depende de parámetros externos y variables, como el espacio y material disponibles durante el crecimiento. Así, por ejemplo, si numerosos cristales se van formando simultáneamente en un espacio pequeño, la competencia entre ellos puede hacer que se deformen unos a otros, dando formas incompletas o contorsionadas.
Un ejemplo particularmente interesante es el caso de las maclas (cristales que crecen juntos como siameses, digamos) y que veremos en otra oportunidad.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.
P.S.: La imagen de la figura 1 es de este sitio. A la figura 2, la tomé de aquí.
Publicado en Geología para principiantes, Geología para todos | 
Etiquetas: Minerales | 
No hay comentarios »
Así está mi dinosaurio, casi listo para nacer.
Hola, chicos, ¿vienen siguiendo mi juego con el dino que está preparándose a salir del cascarón? Aquí llevaba 24 horas el juguetito en remojo, ¡y miren cómo ya empiezan a verse grietas en el cascarón!
Yo estoy ansiosa por verlo «nacer» ¿y ustedes? ¡Creo que el próximo viernes ya será un hecho! Mientras tanto, pasen el lunes por el blog, para aprender cosas más científicas. Los espero. Graciela.
Oferta para hidrogeólogo
Empresa Patrimonio Consultores está buscando un hidrogeólogo que trabaje como consultor.
Las dimensiones de la Tierra. Hoy Eratóstenes. Parte 2.
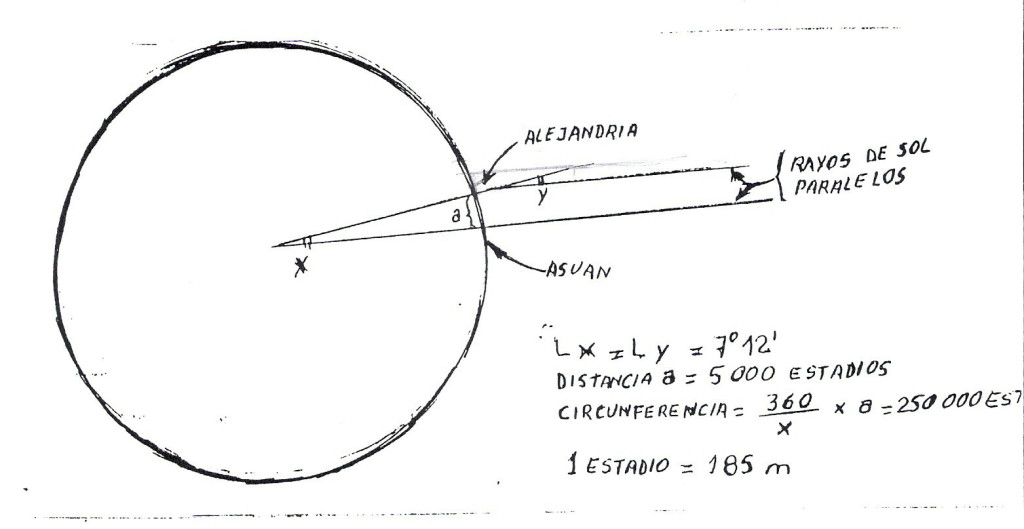
Figura 1
Este post es continuación del de la semana pasada, de modo que deberían empezar por leerlo antes de internarse en el de hoy.
El lunes pasado respondí las siguientes preguntas:
¿Cuáles son las dimensiones más significativas de la Tierra?
¿Qué es un arco de meridiano?
¿Para qué sirve conocer la longitud del arco de meridiano?
¿Quién midió el arco de meridiano por primera vez?
¿Quién fue Eratóstenes?
A partir de aquí, retomamos las preguntas que quedaron pendientes en la primera parte de este post, que publiqué el lunes pasado:
¿Cómo se dio cuenta de que la Tierra era redonda y que podpia medir su circunferencia?
En primer lugar, recordemos que los griegos ya sabían de la esfericidad de la Tierra desde el Siglo V antes de Cristo, en función de observaciones que ya les he comentado antes, pero en el caso particular de Eratóstenes, las pruebas de que se valió fueron relativamente sencillas.
Siendo director de la Biblioteca de Alejandría, Eratóstenes tenía acceso a información muy calificada para la época, y en uno de los tantos papiros en los que esa información se registraba, leyó que en la ciudad de Siena, (hoy llamada Assuán y situada unos 800 km al sureste de Alejandría) los rayos solares al caer sobre una vara el mediodía del solsticio de verano (el actual 21 de junio) no producían sombra alguna.
Picado por la curiosidad, Eratóstenes comenzó a replicar esas observaciones en Alejandría, utilizando la iluminación en un pozo, que era completa siempre en un mismo día y a la misma hora, y se desplazaba, en cambio, dejando parte del pozo en sombras en cualquier otro momento.
No obstante, las horas de sombra cero no coincidían en los registros de ambas ciudades. Ahora bien, asumiendo, muy correctamente que si el Sol se encuentra a una distancia tan grande que es comparativamente infinita respecto a las consignadas en la Tierra, sus rayos son paralelos, ya que se reúnen precisamente en el infinito.
El sabio coninuó un paso más adelante, razonando que si los rayos solares son paralelos, al alcanzar una Tierra plana, como algunos todavía insistían por entonces, no debería haber diferencias entre las sombras proyectadas por los objetos a la misma hora del mismo día, independientemente de la distancia entre ellos. Las diferencias en las sombras sólo podían explicarse sobre una superficie curva, tal como se ve en la Figura 2.
Con esos mismos juegos de distancias y sombras, midió el arco de meridiano que le serviría para establecer en seguida la circunferencia de la Tierra, tal como les expliqué el lunes pasado.
Figura 2
¿Cómo formuló la medición del arco de meridiano?
Con esas observaciones previas como dato inicial, Eratóstenes se valió del razonamiento que les muestro en la Figura 1, para medir el arco de meridiano (a en ese dibujo).
Como pueden ver en el diagrama, los rayos solares, considerados paralelos definen en Siena sombra cero para una estaca, pero en Alejandría, arrojan una sombra con una estaca (que al estar vertical sería como una continuación del radio terrestre), y forman con esa estaca un á¡ngulo ( denominado y en el dibujo), que resulta igual al ángulo interno de la Tierra (x del dibujo) que subtiende al arco a entre Siena y Alejandría, cuya longitud pretendía medir.
Los ángulos x e y son iguales, precisamente porque son ángulos correspondientes entre paralelas, y un teorema ya existente había demostrado ese postulado.
En definitiva, para conocer el valor de x, bastaba con medir y. Grande es la tentación de asumir que Eratóstenes se valió de la resolución trigonométrica del triángulo rectángulo entre los rayos, la estaca y su sombra…pero no. No se conocían los valores trigonométricos por entonces, de modo que utilizó un antiguo aparato denominado gnomon, y logró el valor de 7° 12′ para el ángulo y, exactamente igual a x.
Lo que siguió fue medir la distancia entre Siena y Alejandría, lo cual no se sabe exactamente cómo se realizó, tal vez contratando uno o más esclavos, como es la teoría más elegida; o encargando la cuenta a tropas que marchaban entre ambas ciudades, o a caravanas comerciales. Cualquiera haya sido el modo, Eratóstenes conoció también la distancia a, medida en estadios, como era lo normal en la época.
Con los valores de x y a ya en la bolsa, sólo tuvo que aplicar la fórmula que les puse en el dibujo, y que les expliqué la semana pasada, para conocer el perímetro de la cicunferencia terrestre.
¿Qué valor obtuvo?
Eratóstenes obtuvo un valor de aproximdamente 250.000 estadios, siendo la medida del estadio de 185 m. En definitiva, trasladando ese valor a las medidas actuales, el resultado es de 46.250 km.
¿Cuál es el valor que hoy consideramos el más preciso para la circunferencia de la Tierra?
Hoy se redondea y promedia el valor del perímetro de la circunferencia terrestre en 40.000 km, lo cual, si se considera la diferencia sideral entre los aparatos y métodos usados, asombra por su bajo error comparativo.
Como un plus más a la admiración que Eratóstenes nos provoca, es bueno recordar que él continuó por muchos años midiendo otros arcos de meridiano, y al encontrar variaciones significativas entre sus resultados, fue uno de los primeros en sugerir que la forma de la Tierra no era la de una esfera perfecta. En efecto, en una esfera perfecta, todos los ángulos iguales subtienden arcos iguales, cosa que no se reflejaba en sus calculos.
Para confirmar esta apreciación habrían de transcurrir por lo menos diecinueve siglos, pero eso ya es tema para otros posts.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.