Archivo de la categoría ‘Geología para principiantes’
Un mineral más
Hoy les presento una foto tomada de la página institucional de la Secretaría de Minería de Córdoba, en la que se pueden ver características del feldespato.


La ley de Stokes, sus derivaciones y aplicaciones.
 En un post anterior, les conté que buena parte de la dinámica del transporte de partículas en medios fluidos se rige por dos principios fundamentales: el que se expresa en la curva de Hjulström, que les expliqué en ese momento; y la ley de Stokes y sus formulaciones derivadas, que les prometí para otro momento.
En un post anterior, les conté que buena parte de la dinámica del transporte de partículas en medios fluidos se rige por dos principios fundamentales: el que se expresa en la curva de Hjulström, que les expliqué en ese momento; y la ley de Stokes y sus formulaciones derivadas, que les prometí para otro momento.
Esa promesa, es la que vengo hoy a cumplir.
¿Quién fue Stokes?
Sir George Gabriel Stokes nació en Irlanda el 13 de agosto de 1819, y murió en 1903, tras una larga vida dedicada a las ciencias matemáticas y físicas, en las que hizo aportes tan valiosos como el que aquí comentamos en relación con la dinámica de fluidos.
Sus aportes científicos lo hicieron acreedor de numerosos honores en todo el mundo, y a lo largo del tiempo. Entre otras cosas, fue secretario y luego presidente de la Royal Society de Inglaterra, de la que era miembro desde 1851, y la cual le otorgó la Medalla Rumford en 1852, por sus estudios sobre la longitud de onda de la luz; y en 1893, también la Medalla Copley. Esta última constituye el premio académico más antiguo que concede una institución académica, ya que la primera entrega fue en 1731.
En 1869 presidió la reunión de la BAAS (British Association for the Advancement of Science, que traducido significa Asociación Británica para el Avance de la Ciencia) en Exeter. Entre 1883 y 1885 fue designado como conferencista Burnett en la Universidad de Aberdeen. Este es un honor que concede a científicos destacados, la Fundación Burnett creada por el comerciante John Burnett, nativo de Aberdeen, Escocia, quien a su muerte acaecida en 1784, había legado toda su fortuna y posesiones para propósitos filantrópicos.
En 1889 fue nombrado baronet, y recibió a lo largo de su vida, numerosos doctorados honoríficos otorgados por muchas universidades,y fue seleccionado como miembro de la Orden Pour le Mérite de Prusia.
Pero tal vez el honor más universal, duradero y conocido es el haber atribuido su nombre (Stoke) a la unidad de viscosidad cinemática en el Sistema Cegesimal de Unidades.
¿A qué se refiere la ley de Stokes, y cómo es su formulación?
La ley de Stokes, formulada en 1851, describe matemáticamente la fuerza de fricción experimentada por objetos esféricos que se desplazan en el seno de un fluido viscoso en un régimen laminar; y reconoce como antecedente a las ecuaciones de Navier-Stokes.
Dicho en otras palabras, se reconoce que sobre todo cuerpo que se mueve en un fluido viscoso, se ejerce una fuerza resistente que se opone al movimiento, y que la Ley de Stokes calcula para cuerpos esféricos, según la siguiente fórmula:
F d = 6 r· v.μ
Donde F es la fuerza ejercida por la fricción, r es el radio de la esfera en movimiento, v su velocidad y μ la viscosidad del fluido en el que está inmersa la partícula. Por supuesto, 6π es una constante, es decir seis veces el número pi.
Aclaremos ahora el concepto de viscosidad de un fluido que no es más que la medida de su resistencia a las deformaciones graduales producidas por tensiones, ya sea cortantes o de tracción. En el lenguaje corriente, es lo que expresamos al decir cuánto más o menos espeso es un fluido, sobre todo un líquido.
¿Cuáles son las limitaciones para la verificación de la ley en sistemas naturales?
La ley de Stokes fue calculada y formulada para el movimiento de partículas esféricas pequeñas, y moviéndose a velocidades bajas, en condiciones de flujo laminar, es decir con números de Reynolds bajos.
Si no se cumplen todas esas condiciones o requisitos, la fórmula pierde precisión. Por cada elemento que cambia, se van introduciendo errores en el resultado final. En la naturaleza, a diferencia de lo que ocurre en un laboratorio, esos errores siempre están presentes, porque no hay partículas sedimentarias naturales que sean perfectamente esféricas; ni flujos permanentemente laminares, ya que la introducción de las irregularidades que siempre hay en los cauces, y las variaciones lógicas de caudal, generan flujos que pueden cambiar de carácter en pocos metros o en poco tiempo.
¿Qué otros principios derivan de la ley de Stokes?
Puede reemplazarse el sistema compuesto por partículas que avanzan a favor de un flujo laminar, por otro equivalente, en el que las partículas (teóricamente esféricas, y muy pequeñas) caen verticalmente en un fluido viscoso debido a su propio peso.
En tal situación, puede calcularse su velocidad de caída o sedimentación, que en el punto en que se iguala la fuerza de fricción más el empuje de Arquímedes, con el peso aparente de la partícula en el fluido, se vuelve constante, y es conocida como velocidad límite, y responde a una fórmula que contempla la densidad del cuerpo y la del fluido, y en la que el primer miembro de la ecuación representa el peso de la esfera. En el segundo miembro de la ecuación, el primer término responde al empuje del fluido, y el segundo, a la fuerza resistente.
A través de sucesivos pasos matemáticos (con los que no los quiero complicar) se alcanza la fórmula de la velocidad de caída de una partícula en un fluido que resulta ser:
donde:
- V s es la velocidad de caída de las partículas o velocidad límite.
- g es la aceleración de la gravedad.
- ρp es la densidad de las partículas.
- ρf es la densidad del fluido.
- η es la viscosidad del fluido.
- r es el radio equivalente de la partícula, entendiéndose por radio equivalente de una partícula natural,- casi nunca perfectamente esférica- el de la esfera en la cual la partícula se inscribe más ajustadamente.
- Lo más interresante de esta última ecuación es la clara visualización de que el valor de la velocidad de caída es directamente proporcional al cuadrado del radio de la esfera. Este concepto se aprovecha en aplicaciones de laboratorio para medir texturas.
¿Cuáles son las aplicaciones prácticas de estos principios?
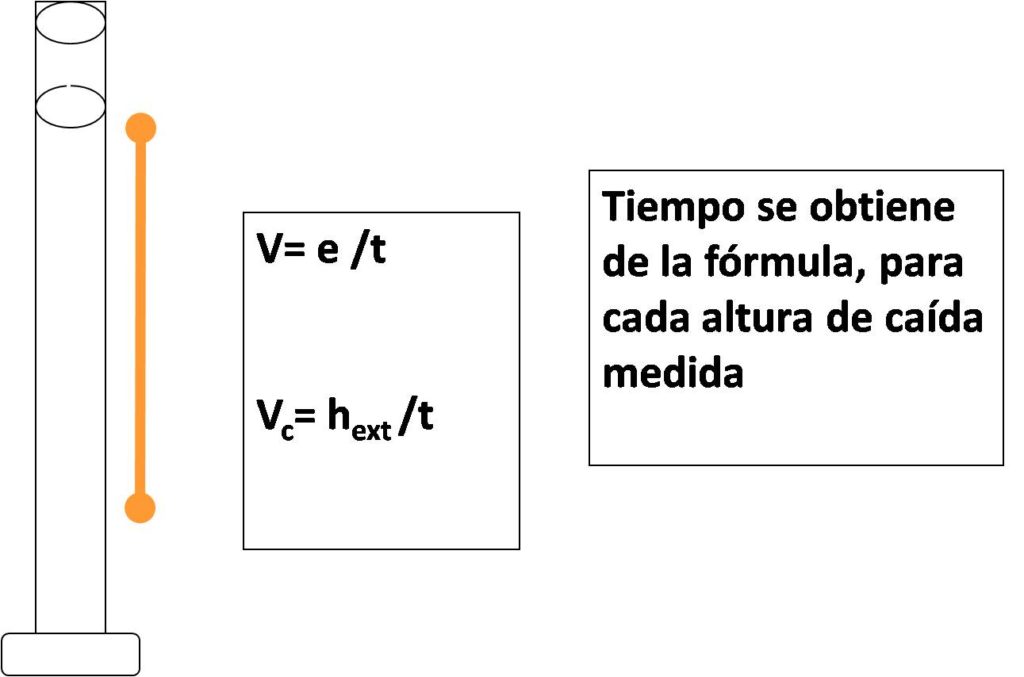
Los postulados de la ley de Stokes y sus derivaciones, se aprovechan para medir viscosidadad mediante el uso de viscosímetros de esfera en caída libre.
Colaboran también para la mejor comprensión de los procesos de sedimentación de pequeñas partículas, tanto en medios acuáticos como aéreos, es decir, en la atmósfera, donde puede calcularse el tiempo de permanencia en suspensión de determinados polutantes
Ya dijimos que además es la ley que se aplica para determinar el porcentaje de cada intervalo de materiales de granulometría muy fina que participan de la composición de un suelo o su sedimento, lo cual se hace mediante el ensayo de sedimentación.
El método de medición de texturas aplicando esta ley, está exhaustivamente explicado en el apunte correspondiente que he subido en su momento en este mismo blog.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.
Morfometría de formas elementales
 Tal como prometí hace algunos lunes, hoy subo una continuación de los conceptos básicos sobre Geomorfología cuantitativa. En este caso, se trata de la medición de geoformas de menor dimensión, conocidas como elementales. Se trata de las unidades menores del paisaje a analizar.
Tal como prometí hace algunos lunes, hoy subo una continuación de los conceptos básicos sobre Geomorfología cuantitativa. En este caso, se trata de la medición de geoformas de menor dimensión, conocidas como elementales. Se trata de las unidades menores del paisaje a analizar.
¿Qué se cuantifica con la morfometría de formas elementales?
Esta parte de la Geomorfología cuantitativa registra las medidas de las unidades de relieve de menor extensión, tales como colinas individuales, depresiones, interfluvios acotados, etc., en los que pueden generalizarse los resultados de unas pocas mediciones, porque el paisaje presenta homogeneidad.
¿Por qué resulta tan importante a la hora de describir el paisaje?
Porque en las mediciones propias de la orometría, que definimos en el post que presenté hace varias semanas, al estar referidas a grandes espacios, los valores numéricos, por más precisos que sean, enmascaran siempre gran cantidad de rasgos particulares, que se pierden en los números, generalmente promedios, que se toman como representativos de la generalidad.
El alto grado de complejidad que necesariamente caracteriza las áreas mayores, se pierde en una abstracción numérica. Por eso, la descripción particular de cada una de las unidades presentes en un paisaje dado, arroja un cuadro más fiel, y un mejor reflejo del relieve real. Eso es lo que -a diferencia de la orometría- proporciona la morfometría, es decir la cuantificación de las formas elementales.
¿Qué partes incluye la morfometría?
Esencialmente incluye dos aproximaciones diferentes: la medición de las laderas, y la de las redes de drenaje, o hidromorfometría. Esta última, en un sentido más estricto, no se ocupa exactamente de formas elementales sino de los cursos de agua que conforman cuencas y subcuencas; y que por ende representarían espacios de dimensión intermedia entre los que conciernen a la orometría por un lado, y a las formas elementales por el otro.
Hoy nos ocuparemos de la morfometría de laderas, y la hidromorfometría será motivo de un post futuro.
¿Qué se mide de forma directa en las laderas?
La medición por excelencia para una ladera, es su pendiente, la que se realiza en el campo, ya sea con clinómetro o con el eclímetro de la brújula geológica. Por supuesto hay también otras mediciones, como su longitud, o las alturas relativas y absolutas, todas las cuales se interrelacionan. Pero iremos por partes, en diversos posts.
La pendiente, expresa la inclinación de la superficie del relieve, con respecto a un plano horizontal ideal. Puede expresarse en porcentaje, es decir la cantidad de metros que se asciende o desciende a lo largo de 100 metros de distancia horizontal.
La otra alternativa es la medición directa de un ángulo, que se expresa en grados y que puede ser positivo si se trata de una elevación, o negativo, al tratarse de una depresión.
Hay determinados procesos geomorfológicos que se relacionan con rangos muy definidos de valores de pendiente, ya que ésta influye directamente en la velocidad del escurrimiento, en la estabilidad o falta de ella de los materiales que la componen, o en la posibilidad o no del desarrollo de suelos evolucionados.
Por cierto, para comprender los procesos, estos valores no son suficientes por sí mismos, ya que también hay influencias de la orientación (por la mayor o menor exposición al sol y a los vientos dominantes), de la cubierta vegetal, de la composición litológica, etc.
¿Qué tratamiento puede darse luego a los valores obtenidos?
Por un lado, las medidas mismas pueden obtenerse no sólo en el campo, sino también sobre la base de cartas topográficas que proporcionan curvas de nivel, (que definimos ya en el post sobre orometría).
Por otro lado, a partir de esas medidas puede obtenerse otra gran cantidad de información matemática.
Vayamos por partes:
La pendiente media de una geoforma puede obtenerse calculándola por la diferencia entre las cotas máxima y mínima de las curvas que la representan, en relación con la distancia horizontal que las separa. La pendiente máxima, en cambio se obtiene entre las dos curvas más próximas entre sí. No se asusten, en otros posts haremos hincapié en estas formas de cálculo, y hablaremos con mucho detalle sobre las curvas de nivel.
Los promedios obtenidos de la morfometría de formas elementales, pueden conducir a su vez a la generalización orométrica de espacios más extensos. Para ello no se requiere medir todas las formas elementales, sino las que se seleccionen según una grilla con cuadros de igual tamaño, de modo que representen al conjunto sin elecciones arbitrarias ni sesgadas.
Una vez que se cuenta con un número suficiente de datos morfométricos, la extensión de los mismos para caracterizar grandes espacios, permite obtener la media aritmética, que es en sí misma demasiado abstracta, razón por la cual se recurre al análisis de frecuencia.
Ese análisis se obtiene en el histograma que ya hemos descrito en el otro post, al hablar de las curvas hipsométricas. Digamos que en el histograma, cada clase de altitud, está representada por un segmento que es más largo cuanto mayor frecuencia de geoformas de esa altitud hayan sido relevadas.
Desde ese histograma se construyen también las curvas acumulativas que a su vez arrojan datos como el modo (la altitud más frecuente) y la mediana, que separa en dos números iguales, las geoformas de mayor altitud que ella y las de menor altura. En otras palabras es el punto medio de la frecuencia.
Otra de las construcciones que pueden hacerse desde las mediciones mencionadas, es la curva clinográfica.
¿Qué es una curva clinográfica?
Es la curva que representa la repartición de las pendientes medias por cada intervalo de altitud.
Se obtiene sobre ejes ortogonales, donde en el eje X (el horizontal) se coloca la distancia media entre las curvas de nivel, que se obtiene a su vez dividiendo la superficie comprendida entre dos curvas consecutivas, por la mitad de la suma de las longitudes de ambas; y en el eje Y (el vertical), el valor de la altitud.
¿Qué formas pueden afectar las laderas, y cómo se las define?
Cada ladera no tiene necesariamente el mismo valor de pendiente a lo largo de todo su perfil, de allí que se la suela dividir en segmentos, siguiendo los puntos de ruptura (es decir de cambio) perceptibles, y luego se puede caracterizar la forma resultante.
Existen pues, perfiles planos, ya sea horizontales, verticales o inclinados; cóncavos; convexos; convexo-cóncavos; convexo-rectilíneo-cóncavos; regulares o irregulares. Casi todos se relacionan con procesos y paisajes bien definidos, pero eso ya escapa al tema de este encuentro de hoy.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.
P.S.: La foto que ilustra el post es de la isla de M’orea, en la Polinesia Francesa. Un paraíso en la Tierra.
Mini glosario geológico
 El lunes pasado, subí para ustedes un apunte en el que reseñé muy brevemente el desarrollo de las Ciencias Geológicas a lo largo del tiempo, y allí les prometí que hoy subiría el glosario de términos que requerirían para una cabal comprensión de los temas entonces tratados.
El lunes pasado, subí para ustedes un apunte en el que reseñé muy brevemente el desarrollo de las Ciencias Geológicas a lo largo del tiempo, y allí les prometí que hoy subiría el glosario de términos que requerirían para una cabal comprensión de los temas entonces tratados.
Aquí cumplo mi promesa.
glosario 1 by Graciela L. Argüello on Scribd
Nos vemos el miércoles. Graciela.
El interior terrestre, las discontinuidades sísmicas.
 Hoy vamos a avanzar un poco más sobre el conocimiento del interior terrestre, pero para poder comprender lo que voy a presentarles en seguida, deben necesariamente revisar los conceptos que subí en este post, y sin los cuales, lo que sigue les parecerá chino básico. También deberán recordar las características de las ondas sísmicas que les expliqué aquí. Sólo continúen leyendo este post, después de haber ido a leer las nociones previas en los otros dos linkeados arriba.
Hoy vamos a avanzar un poco más sobre el conocimiento del interior terrestre, pero para poder comprender lo que voy a presentarles en seguida, deben necesariamente revisar los conceptos que subí en este post, y sin los cuales, lo que sigue les parecerá chino básico. También deberán recordar las características de las ondas sísmicas que les expliqué aquí. Sólo continúen leyendo este post, después de haber ido a leer las nociones previas en los otros dos linkeados arriba.
¿Qué se entiende por discontinuidades sísmicas?
Si me han hecho caso, y fueron a leer los conceptos previos, ya saben que las diversas ondas que se generan en terremotos, tienen velocidades de propagación que dependen básicamente de las condiciones del medio que atraviesan, y que normalmente crecen cuanto más densos son los materiales por los que viajan. La inmediata conclusión es que debido a la compresión que ejercen los cuerpos sobreyacentes, las rocas son más compactas cuanto más profundas sean.
Por ende cabe esperar que las velocidades de propagación de cada tipo de ondas, vayan creciendo progresivamente a medida que aumenta la profundidad del medio por el que se transmiten. Cuando esa secuencia lógica de velocidades crecientes, se ve interrumpida, ya sea por inversiones de velocidad, o por saltos abruptos en el incremento esperado, se habla de lo que se conoce como discontinuidad sísmica.
¿Cuál fue la primera discontinuidad en conocerse, y qué importancia tiene?
En el año 1909, el sismólogo croata Andrija Mohorovicic (1857-1936), hizo un importante descubrimiento al estudiar registros obtenidos por los sismógrafos durante el sismo acontecido en el valle de Kulpa, en Yugoslavia.
Él observó que a distancias comprendidas entre 200 y 720 km del epicentro, los sismogramas que se obtenían revelaban notorios cambios de velocidad tanto en las ondas P como en las S. El científico relacionó rápidamente esas diferencias de velocidad con una variación significativa en los materiales atravesados por dichas ondas, correspondiendo a rocas de mayor densidad por abajo del cambio, y menos densas por encima de él. La línea límite de los saltos de velocidad, fue denominada como discontinuidad sísmica y ubicada a una profundidad de alrededor de 40 km, aunque era más profunda bajo los continentes, y más somera bajo los océanos.
Esa diferencia de profundidades bajo continentes y océanos es de gran relevancia para cosas que veremos después, por favor, no dejen de tomar nota de esto.
Con posterioridad, otros investigadores confirieron a la discontinuidad el nombre de «Discontinuidad de Mohorovicic», en homenaje a su descubridor. Lamentablemente, es más conocida por su apócope de «Moho».
¿Qué discontinuidad se conoció luego, y cómo fue el proceso de interpretación?
Ahora se pone interesante la cosa. Veamos por qué.
El descubrimiento se debe a Beno Gutenberg, sismólogo nacido en Darmstadt, Imperio Alemán, el 4 de junio de 1889, y fallecido el 25 de enero de 1960. Se doctoró en la Universidad de Göttingen en 1911, y fue su director de tesis el profesor Emil Johann Wiechert, que volveremos a mencionar más abajo. Fue docente en las Universidades de Estrasburgo y de Frankfurt am Main, y más tarde en el Instituto Tecnológico de California.
Ahora, ya sabiendo de quién hablamos, presten mucha atención a la figura que ilustra el post, porque en ella veremos las cosas más claramente.
Cuando Gutenberg contaba con apenas 24 años, se dedicó a observar los sismogramas obtenidos en diversos sismógrafos de una red «mundial», todavía bastante incipiente. Así pudo comprobar que si se proyectaban los epicentros de distintos terremotos, sobre la representación de un corte del globo terrestre (idealizado como un círculo atravesado por los distintos tipos de onda, según se ve en la figura, a la izquierda) se repetía un interesante fenómeno.
Vean ahora las dos esquematizaciones arriba y a la derecha en el gráfico. En un sismo cualquiera, si se leen sismogramas obtenidos en los sismógrafos ubicados en zonas opuestas de la Tierra, desde una posición aproximada a los 103° y hasta alrededor de los 257° (a lo largo de un desplazamiento superficial en la circunferencia ideal), sólo se reciben ondas P, mientras que las ondas S desaparecen, cambiando su modo de vibración al de las P.
Si recuerdan (ya los mandé a leer esa explicación, me imagino que cumplieron la consigna) que las ondas P se transmiten en todos los estados de la materia, mientras que las S sólo lo hacen en medios sólidos; podría deducirse que hay un cuerpo no sólido interpuesto, generando un «cono de sombra» que impide que en los sismógrafos de las áreas entre 103 y 257° del epicentro, se registren ondas S. Eso es lo que quise representar con el rayado horizontal en el primero de los esquemas de la parte superior derecha de la figura.
En el segundo esquema, repito la experiencia de Gutenberg, quien fue analizando sismos con diferentes epicentros, pero en los que se repetía siempre el mismo patrón. En un segundo caso, el cono de sombra ya no es tal, porque se reduce a las zonas en que las líneas de los dos conos de dos sismos distintos se cruzan (observen el espacio en que se superponen las dos direcciones de rayado). Si esto se repite un número suficiente de veces (parte de abajo a la derecha de la figura), se va delimitando, no ya un cono, sino un círculo de posición central (parte derecha de la figura), en el que las ondas S no se transmiten como tales, sino que pasan a comportarse como ondas P.
Así fue que en 1913, Beno Gutenberg pudo deducir que existía un núcleo terrestre no sólido, cuyo límite estaba situado en una discontinuidad sísmica localizada a aproximadamente 2.900 km de profundidad. Esa discontinuidad que limita el núcleo terrestre, hoy lleva el nombre de su descubridor, es decir, Discontinuidad de Gutenberg.
¿Qué es la discontinuidad de Conrad?
Ya con la metodología de análisis bien establecida por Gutenberg y Mohorovicic, los estudios posteriores definieron una nueva discontinuidad algo más superficial que el Moho, que se estableció en 1923, y que aparece entre unos 10 y 25 km por debajo de los continentes. Este límite, conocido como Discontinuidad de Conrad, permite reconocer diferencias fundamentales entre los fondos continentales, también conocidos como siálicos, en referencia al apócope Sial, que responde a su composición dominante de Sílice y Aluminio; y los fondos oceánicos, también llamados simaicos, en referencia a la palabra Sima, que indica la composición mayoritariamente de Sílice y Magnesio, propia de las rocas submarinas. Pero sobre todo esto ya hablaremos en un post específico.
¿Cuál fue la siguiente discontinuidad que se descubrió?
Estudios más recientes, llegaron a definir a unos 5.200 km de profundidad, una nueva discontinuidad que señala el límite entre el núcleo externo en estado fundido o semipastoso (en el que las ondas S dejan de comportarse como tales), y el núcleo interno sólido de la Tierra.
El descubrimiento se debe al trabajo conjunto de Wiechert, (el maestro de Gutenberg) Lehmann y Jeffrys, y se produjo en 1936. Hoy esa irregularidad se conoce como Discontinuidad de Lehmann, en homenaje a la sismóloga danesa Inge Lehmann, que llevó la mayor carga en las investigaciones.
¿Cuál fue la última discontinuidad que se conoció?
En tiempos más cercanos al presente, pudo reconocerse un marcado decrecimiento de la velocidad de las ondas sísmicas a alrededor de 100 km de profundidad. Esto está en total oposición a la tendencia a la aceleración por la mayor compactación esperable en profundidad, y resultó ser un descubrimiento muy interesante, en la década de los 60, que abriría el camino a numerosas explicaciones de las que echaremos mano más adelante. Esa capa de baja velocidad se dio en llamar astenósfera, y no aparece en todo el planeta, como tampoco lo hace la discontinuidad de Conrad, a diferencia de las restantes.
¿Qué se concluyó de todo esto?
Una vez reunida toda la información precedente, los científicos estuvieron al fin listos para presentar la interpretación debidamente fundamentada de la estructura interna de la Tierra, con las geósferas que la componen, y que bien se funden con las geósferas externas, que no son sino las que integran la atmósfera. Pero esos serán temas a tratar en nuevos posts. Tengan paciencia.
Si este post les ha gustado como para llevarlo a su blog, o a la red social, por favor, mencionen la fuente porque esta página está registrada con IBSN 04-10-1952-01.
Un abrazo y hasta el miércoles. Graciela.